Tenseur - Définition

Introduction

En mathématiques, plus précisément en algèbre multilinéaire et en géométrie différentielle, un tenseur désigne une fonction multilinéaire. En physique et en sciences de l'ingénieur, les tenseurs sont utilisés pour décrire et manipuler diverses grandeurs et propriétés physiques comme le champ électrique, la permittivité, la déformation etc.

Par extension, on utilise souvent le terme tenseur pour désigner un champ de tenseurs, c'est-à-dire une application qui associe à chaque point d'un espace géométrique un tenseur différent.

La première utilisation de la notion et du terme de tenseur s'est faite dans le cadre de la mécanique du continu, en relation avec la nécessité de décrire les contraintes et les déformations subies par les corps étendus, à partir de laquelle fut formalisée la mécanique rationnelle.

Les tenseurs sont largement utilisés dans la relativité générale, pour décrire rigoureusement l'espace-temps comme variété courbe quadri-dimensionnelle. Les tenseurs sont utilisés dans de nombreux autres domaines de la physique, y compris l'électromagnétisme, la mécanique des fluides et mécanique du solide. En particulier, le tenseur des contraintes et le tenseur des déformations sont utilisés dans la science des constructions pour définir l'état de tension et de déformation en tout point d'une structure.

Les tenseurs sont également utilisés en géométrie différentielle pour définir sur une variété différentielle les notions géométriques de distance, d'angle et de volume. Cela se fait par le choix d'un tenseur métrique, c'est-à-dire un produit scalaire défini sur l'espace tangent de chaque point. Grâce à ce concept, sont alors définies et étudiées les questions liées à la courbure de la variété. D'autres tenseurs, tels que le tenseur de Riemann et le tenseur de Ricci, sont des outils importants pour cette étude.

Introduction

Les composants du tenseur des contraintes, un tenseur de deuxième ordre, en trois dimensions. Le tenseur dans l'image est le vecteur ligne des forces agissants sur les faces X, Y et Z du cube. Ces forces sont représentées par des vecteurs colonnes. Les vecteurs ligne et colonnes qui composent le tenseur peuvent être représentées par une matrice :

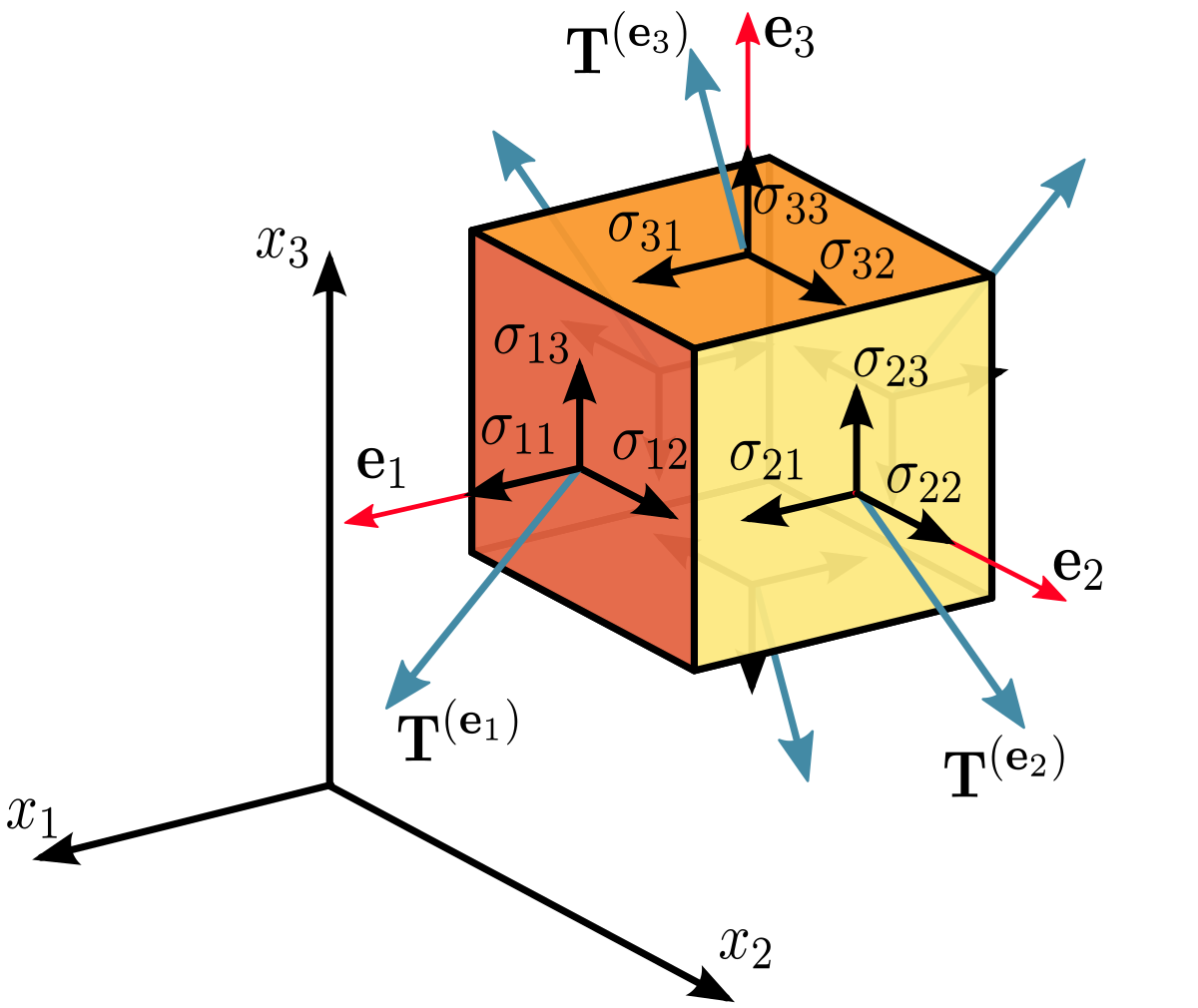
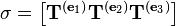
D'un point de vue physique, un tenseur est un objet très général, défini intrinsèquement à partir d'un espace vectoriel V (qui peut être par exemple l'espace euclidien tridimensionnel, ou bien l'espace-temps quadri-dimensionnel) et qui ne dépend pas d'un système de coordonnées particulier.

Par rapport à un système de coordonnées fixé, un vecteur de l'espace s'exprime comme une suite finie de nombres (ce sont les composantes du vecteur), soit : un n-uplet. Si on change de système de coordonnées, ce vecteur s'exprimera alors par un autre n-uplet, différent selon une loi bien précise. Un tenseur, exprimé dans un système de coordonnées particulier, est une sorte de n-uplet généralisé qui peut avoir 1 dimension (un n-uplet), ou 2 (une matrice) ou plus. Par un changement du système de coordonnées, les composantes d'un tenseur, comme celles d'un vecteur, sont modifiées par une loi précise.

Cette notion physique de tenseur comme « objet indépendant du système de coordonnées » est utile pour exprimer beaucoup de lois physiques, qui par leur nature ne dépendent pas des systèmes de coordonnées choisis. La notion mathématique d'un tenseur est réalisée d'une manière plus rigoureuse par l'algèbre multilinéaire. Dans le langage de l'algèbre linéaire, un système de coordonnées est une base et la loi de transformation est fournie par une matrice de changement de base. En outre, la définition d'un tenseur peut être donnée sans faire référence aux systèmes de coordonnées (aux bases), en utilisant la notion d'application multilinéaire et d'espace vectoriel dual.