Identité de MacWilliams - Définition
La liste des auteurs de cet article est disponible ici.
Identité de MacWilliams
Avec les notations du paragraphe précédent, si Q[X] désigne le polynôme énumérateur des poids du code dual de C, alors l'égalité suivante est vérifiée :
![Q[X]=\frac 1{d^k}\Big( 1 + (d-1)X\Big)^n P\Big(\frac{1-X}{1 + (d-1)X} \Big)\;](https://static.techno-science.net/illustrationWebp/Definitions/autres/3/34884eb956ef798b3f3f3223bb5b935f_7c7761fec3ad35b24c9b0aedb38e97ee.png)
Considérons la fonction g de Fdn dans C[X] l'anneau des polynômes à coefficients complexes, définie par :
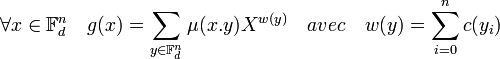
Ici c désigne la fonction de Fd dans C qui à 0 associe 0 et à tout autre élément associe 1. L'application w correspond donc à la fonction poids de Hamming. Une fois encore, (yi) désigne les différentes coordonnées de y dans la base canonique de Fdn.
-
- Le polynôme Q[X], défini par l'égalité suivante, est le polynôme énumérateur des poids du code dual de C.
![Q[X] = \frac 1{q^k} \sum_{c \in C} g(c) \;](https://static.techno-science.net/illustrationWebp/Definitions/autres/4/4326805d7d408258c68774ffa823e0e6_948ea786b1ebe1ba2eb11576e29dd862.png)
La définition du polynôme Q[X] montre que :
![Q[X] = \frac 1{q^k} \sum_{c \in C} g(c) = \frac 1{q^k} \sum_{y \in \mathbb F_d^n} \sum_{c \in C} \mu(c.y) X^{w(y)} = \frac 1{q^k} \sum_{y \in \mathbb F_d^n} b_y X^{w(y)} \quad avec \quad b_y = \sum_{c \in C} \mu(c.y) \;](https://static.techno-science.net/illustrationWebp/Definitions/autres/b/b484a566a7672fa8d79fc874aba30d66_8154ae061051fc0bda4920a3049ab96e.png)
Il est donc nécessaire de calculer by. Si y est un élément du code dual, alors c.y est égal à 0 pour tout c élément de C, on en déduit que μ(c.y) est égal à 1 et by est égal au cardinal de C, c'est-à-dire qk. Si y n'est pas élément de C, alors l'application qui à c associe μ(c.y) est un caractère non trivial du groupe (C, + ). Il est donc orthogonal au caractère trivial, cette relation d'orthogonalité exprime le fait que by est nul. On en déduit que :
![Q[X]=\sum_{c \in C^{\perp}} X^{w(c)} \;](https://static.techno-science.net/illustrationWebp/Definitions/autres/c/c8f15409a3eae87c348dbd1478465ef7_97678b3a77484e34bf77eae767c3eaa6.png)
Cette dernière égalité démontre que Q[X] est bien le polynôme annulateur du code dual.
-
- le polynôme Q[X] vérifie l'égalité suivante :
Si (ci) sont les coordonnées de c et (yi) celle de y, alors les égalités suivantes sont vérifiées :
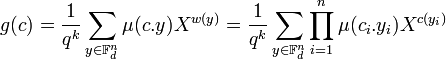
Calculons alors la valeur suivante :
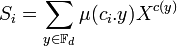
Si ci est nul alors μ(ci.y) est égal à 1 pour toute valeur de y, c(y) vaut 0 si y est nul et 1 sinon, on en déduit que Si = 1 + (q - 1)X. Si ci est non nul alors l'application qui à y associe μ(ci.y) est un caractère non trivial du groupe additif du corps Fd. Il est donc orthogonal au caractère trivial et :
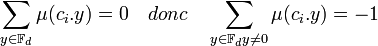
On en déduit les égalités suivantes :
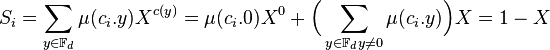
On en déduit l'égalité suivante :
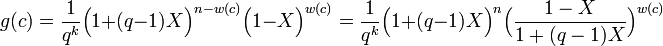
On obtient donc pour expression de Q[X], l'égalité suivante :
![Q[X] = \frac 1{q^k}\Big(1 + (q-1)X \Big)^n \sum_{c \in C} \Big(\frac {1-X}{1 + (q-1)X} \Big)^{w(c)}= \frac 1{d^k}\Big( 1 + (d-1)X\Big)^n P\Big(\frac{1-X}{1 + (d-1)X} \Big)\;](https://static.techno-science.net/illustrationWebp/Definitions/autres/7/79a5d25512a80e9a31eed93d974772a4_c5efdf270b8d67ee66453facaaac2f53.png)
