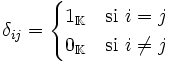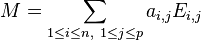Base canonique - Définition

Introduction

Dans un espace vectoriel, une base canonique est une base qui se présente de manière naturelle d'après la manière dont l'espace vectoriel est présenté. C'est ainsi que l'on parle de la base canonique de , de la base canonique de l'espace vectoriel des matrices ou de celui des polynômes.

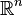
Dans Kn

Définition

Soit un corps et n un entier naturel.

La base canonique de se compose des vecteurs (i variant de 1 à n) définis ainsi :

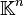
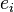
Pour i variant de 1 à n

.

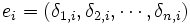
Où désigne le symbole de Kronecker :

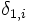
Où le 0 désigne le neutre de la première loi et le 1 celui de la seconde.

Il est important de se rappeler qu'une base a autant de vecteurs que la dimension de l'espace vectoriel.

Exemple

Dans la base canonique est ((1,0,0) , (0,1,0) , (0,0,1)).

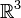
En régle générale la base canonique est définie orthonormée, mais cela ne vaut que pour le produit scalaire canonique. De plus, les coordonnées d'un point (en l'absence de précision) sont données par rapport à cette base, et le produit vectoriel est fait implicitement en déclarant la base canonique directe.

Matrices

La base canonique des matrices est l'ensemble des matrices qui présentent un 1 à l'intersection de la ième avec la jème colonne et 0 partout ailleurs.

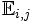
Pour toute matrice M = (a_i,j), ses coordonnées dans la base canonique sont les coefficients

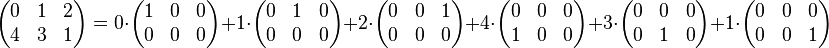
Polynômes

Dans l'anneau des polynômes, la base canonique est la famille de vecteurs .

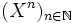
Cette base est infinie.