Orthogonalité - Définition

Introduction

En mathématiques, l'orthogonalité est un concept d'algèbre linéaire associé à une forme bilinéaire. Un cas fréquent est celui où cette forme est un produit scalaire.

Si un espace est munie d'une géométrie euclidienne, il est naturellement équipé d'une distance, deux vecteurs sont orthogonaux si et seulement si leurs directions sont perpendiculaires ou encore forment un angle droit. Depuis la Grèce antique, l'angle droit est à l'origine de la démonstration de nombreux théorèmes. Ceux de Pythagore et de la médiane sont des exemples. Les grands et petits axes d'une ellipse sont orthogonaux, source de multiple propriétés.

L'orthogonalité généralise dans un premier temps l'idée d'angle droit à un espace de dimension finie muni d'un produit scalaire. Les résultats découverts dans l'univers précédent prennent une nouvelle forme. Les axes principaux d'une surface quadrique sont orthogonaux, cette propriété permet leur classification. L'article théorème spectral montre de nombreuses applications, comme la résolution de l'équation du mouvement d'une corde vibrante modélisée par des petites masses en nombre fini et à égales distance ou la méthode des moindres carrés en statistiques.

L'orthogonalité s'applique encore si les nombres sous-jacents ne sont plus réels. L'usage des nombres complexes amène à une autre géométrie, dite hermitienne. En arithmétique, l'utilisation de l'orthogonalité sur les nombres entiers permet à Joseph-Louis Lagrange de trouver une nouvelle démonstration du théorème des deux carrés de Fermat. Les représentations d'un groupe fini font appel à des ensembles de nombres finis. L'orthogonalité y joue un grand rôle.

L'analyse fonctionnelle n'est pas en reste. Il est parfois possible de définir un produit scalaire sur un espace de fonctions à valeurs réelles ou complexes de dimension infinie. L'orthogonalité y est utilisée à travers la notion de base de Hilbert, une généralisation de la base orthonormale. Elle permet de résoudre des équations comme celle de la chaleur ou d'une corde vibrante dans le cas général. Parfois, l'espace de fonctions ne dispose pas de produit scalaire. Le dual topologique permet alors de faire usage de l'orthogonalité. Le crochet de dualité est une forme bilinéaire qui s'applique sur le dual et l'espace, il remplace le produit scalaire et permet d'obtenir des résultats un peu analogues aux configurations précédentes.

Géométrie d'Euclide

Définitions

Une première approche intuitive associe l'orthogonalité à l'angle droit. Dans ce paragraphe E est plan équipé d'une géométrie euclidienne, comme l'angle droit est défini à l'aide de deux droites, et que deux droites sont toujours coplanaires, il n'est pas utile d'aller plus loin. En revanche les résultats s'appliquent encore dans notre espace usuel de dimension trois. Le plan est formalisé soit par les cinq postulats d'Euclide, soit pour être parfaitement rigoureux par les vingt axiomes de Hilbert. E possède des transformations particulières, de E dans lui-même, appelées isométries. Elles conservent les distances. Ainsi, si A et B sont deux points de E et ψ une isométrie, la distance entre ψ(A) et ψ(B) est la même que celle entre A et B. Dans un tel espace, les isométries sont les translations, les rotations et les réflexions correspondant à l'image d'un miroir.

La seule rotation utilisable pour cette définition est celle d'un quart de tour. Il serait possible de définir l'angle droit à l'aide d'une réflexion. Les droites Δ₁ et Δ₂ sont perpendiculaires si et seulement s'il existe une réflexion d'axe Δ₁ laisse globalement invariant Δ₂.

Il est aisé de remarquer que si une droite Δ₂ est perpendiculaire à une droite Δ₁ et si Δ₂ est parallèle à une droite Δ₃, alors les droites Δ₁ et Δ₃ forment un angle droit. La notion d'orthogonalité ne s'applique pas seulement à des droites mais, de manière plus générale à des directions. Deux droites sont dites avoir même direction si et seulement si elles sont parallèles.

Ces deux définitions permettent de nombreuses généralisations. Ainsi deux segments (resp. vecteurs) (resp. bipoints) sont orthogonaux si et seulement si leurs directions le sont. Une droite Δ est perpendiculaire à un plan si et seulement si toute droite du plan est orthogonale à Δ.

Propriétés

Pour la géométrie du triangle, la tradition consiste à utiliser le terme de perpendiculaire et non orthogonal, dans ce contexte, les deux notions sont rigoureusement équivalentes.

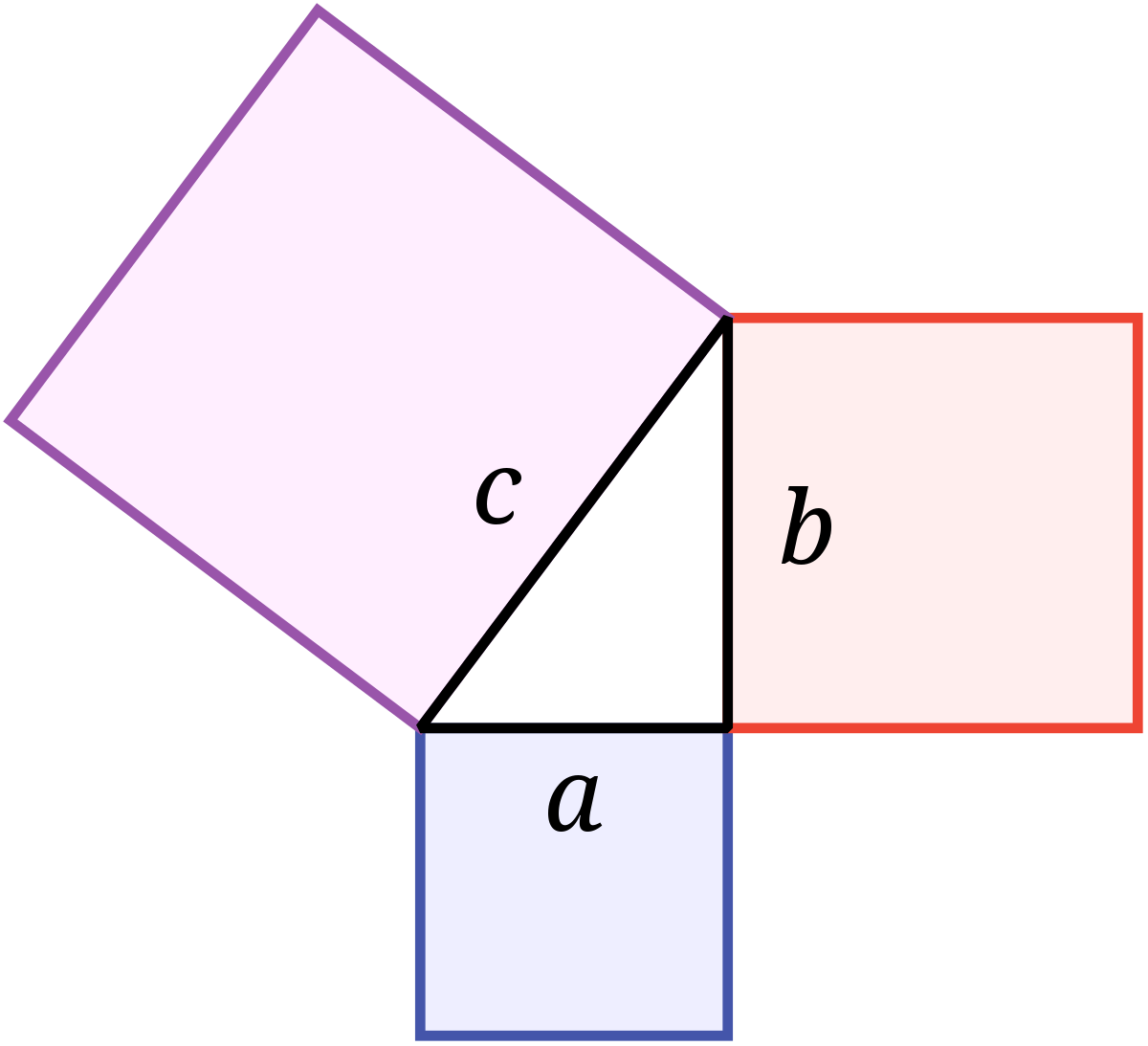
La propriété fondamentale de la géométrie d'Euclide est le théorème de Pythagore. Il s'exprime ainsi :

Ce résultat semble être l'un des tous premiers théorèmes connus de l'humanité. On en trouve probablement des traces à une période datant d'avant l'écriture. La première démonstration connue provient d'Euclide qui vivait autour de -300 av. J.C., elle est rédigée dans un texte nommé les Éléments.

La réciproque est aussi vraie. C'est-à-dire que si, avec les notations de la figure, la somme de l'aire des carré de côté a et b est égal à l'aire du carré de côté c, alors le triangle est rectangle. Autrement dit, si A, B et C sont trois points d'un plan, l'angle formé par les segments [A, B] et [A, C] est droit si et seulement si :

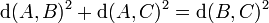
Dans cet article d(A, B) désigne la distance entre A et B.

Cette propriété permet de démontrer le théorème de la médiane attribué à Apollonius de Perga. Il stipule que si A, B et C sont trois points du plan et si I est le milieu du segment [B, C] alors :

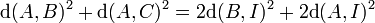
Le terme de médiane désigne une droite passant par un sommet et le milieu du côté opposé d'un triangle. Si un triangle A, B, C est tel que la distance entre A et B est la même que celle entre B et C, le triangle est dit isocèle. Soit I le milieu de A et C, alors le théorème de la médiane indique que :

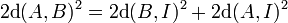
La condition nécessaire et suffisante précédente indiquant qu'un angle est rectangle est remplie et l'angle AIB est droit. Ceci démontre que les deux diagonales d'un losange sont perpendiculaires.

Constructions à la règle et au compas

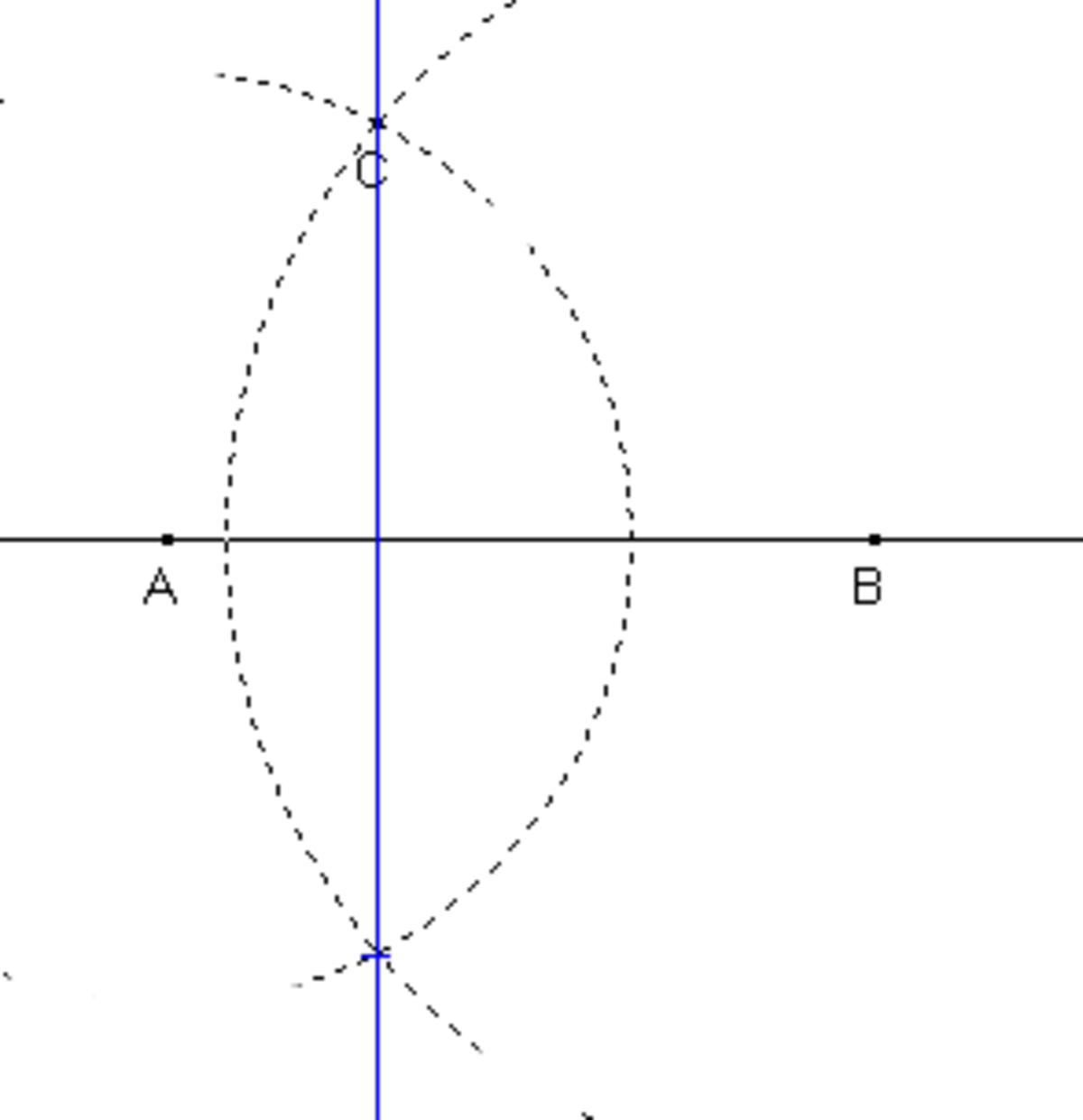
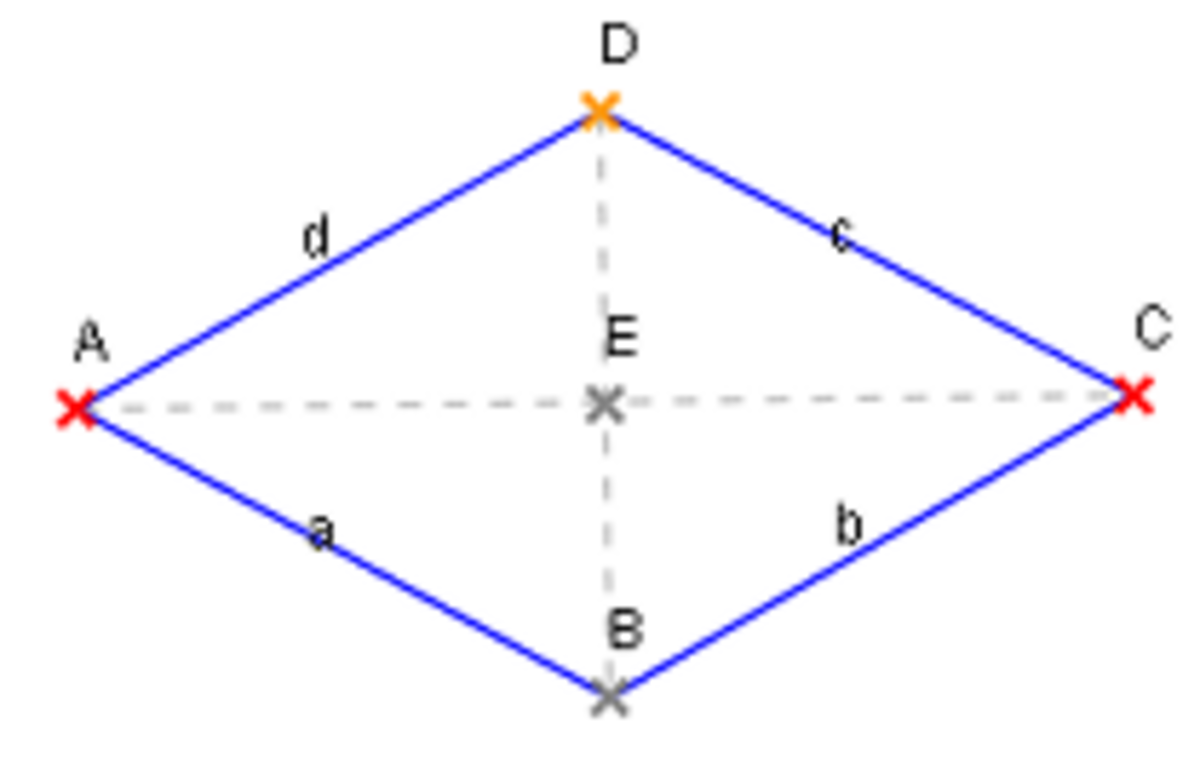
Une première question consiste à savoir comment, à l'aide d'une règle et d'un compas, dessiner deux droites perpendiculaires. Une technique simple consiste à choisir deux points A et B sur la première droite Δ₁ et à dessiner deux cercles de même rayon ayant deux points d'intersections. La droite Δ₁, passant par les deux points d'intersection, est perpendiculaire à la première. La figure est un losange, l'étude des propriétés du paragraphe précédent montre que les deux droites sont perpendiculaires.

La figure de droite montre qu'il est inutile que les deux cercles soit de même rayon. En effet, avec les notations de la figure, soit D le deuxième point d'intersection des deux cercles et O le milieu de C et D. Comme le triangle CAD est isocèle, la droite passant par A et O est perpendiculaire à celle passant par C et D. Un raisonnement analogue montre que la droite passant par B et O possède les mêmes propriétés, elles sont donc les mêmes directions et un point commun O, ce qui montre qu'elles sont confondues avec la droite Δ₁.

Cette technique de construction d'un angle droit est ancienne. Elle date probablement de Œnopide de Chios, un mathématicien grec vivant cinq siècles avant J.C.

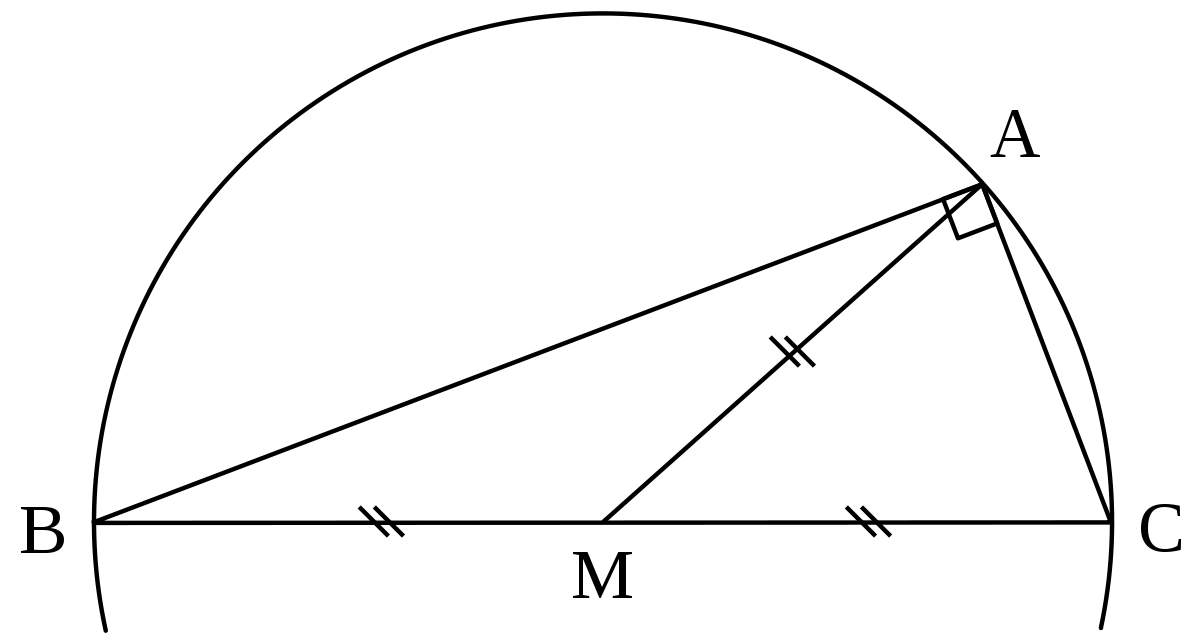
Une autre solution est illustrée par la figure de gauche. Elle consiste à tracer un cercle et un triangle dont un côté est un diamètre et dont le sommet est un point du cercle. Un tel triangle est toujours rectangle. En effet, le théorème de la médiane montre que la somme des carrés des longueurs des segments [A, B] et [A, C] est égal à quatre fois le carré du rayon, c'est-à-dire le carré de la distance entre B et C.

De nombreuses constructions à la règle et au compas utilisent les propriétés de l'orthogonalité. Elle permet de couper un angle en deux, à l'aide de la bissectrice. À l'exception du triangle équilatéral qui n'en a pas besoin, le dessin à la règle et au compas des polygones réguliers constructibles utilise les propriétés de l'orthogonalité.

Orthogonalité et théorèmes géométriques

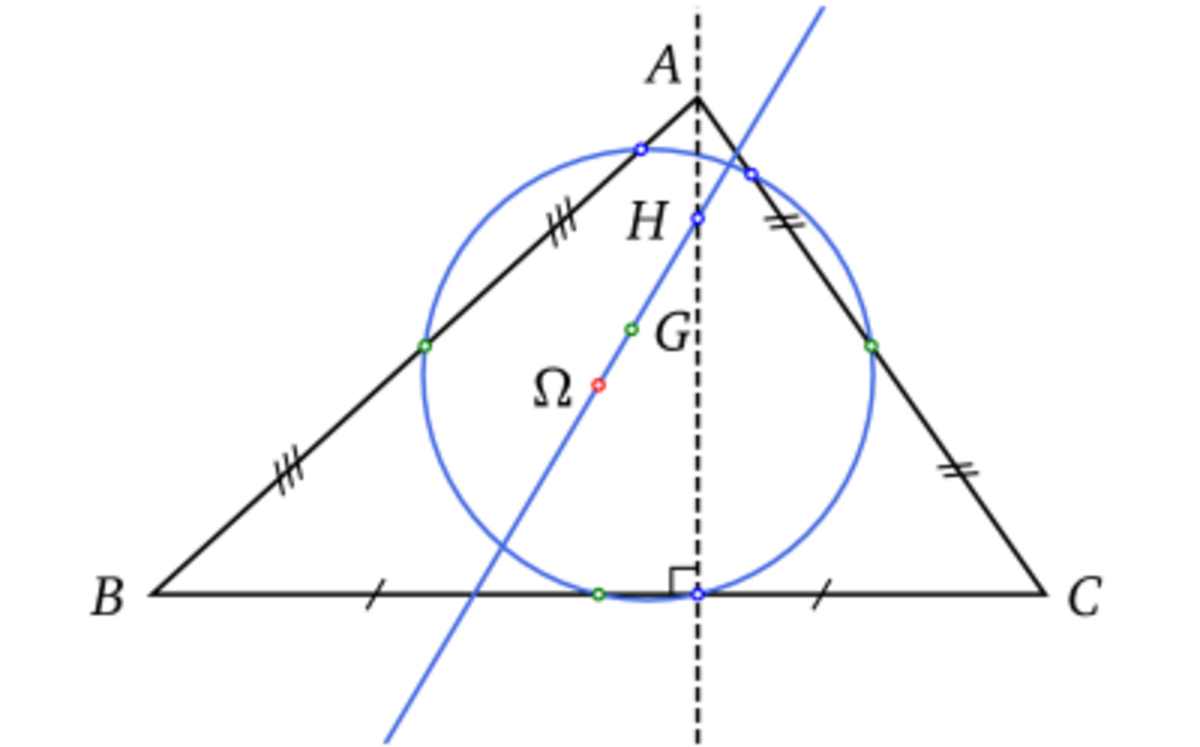
De nombreux théorèmes géométriques utilisent le théorème de Pythagore et donc l'orthogonalité pour pouvoir être démontrés. Le fait que les trois bissectrices d'un triangles soient concourantes et soit le centre du cercle inscrit dans le triangles provient de la propriété d'orthogonalité de la bissectrice déjà rencontrée pour construire deux droites perpendiculaires.

De même, les trois hauteurs d'un triangle d'un triangles sont concourantes. Le point d'intersection s'appelle l'orthocentre. Une hauteur est une droite passant par un sommet et perpendiculaire au côté opposé. Un autre résultat précise que les trois médianes sont aussi concourantes. Le point d'intersection est le centre de gravité. Ce qui signifie que si un triangle est matérialisé en un solide homogène, il est en équilibre sur une pointe posée exactement sur ce point d'intersection. Leonhard Euler trouve une droite remarquable. Le centre de gravité, le centre du cercle inscrit et l'orthocentre sont alignés. Cette droite est le centre d'un cercle étonnant appelé cercle d'Euler. Il passe par neuf points remarquables du triangle. Karl Wilhelm Feuerbach établit son théorème affirmant que le cercle d'Euler est tangent aux trois cercles exinscrits du triangle. Tous ces théorèmes utilisent les propriétés de l'orthogonalité pour pouvoir être démontrées.

Utilisations dans d'autres contextes

L'utilisation de l'orthogonalité en dehors de la géométrie date de la plus haute antiquité. Les babyloniens utilisent un triangle rectangle isocèle de côté un pour calculer la racine de deux. L'orthogonalité d'un angle ainsi que la formule de Héron leur permettaient d'accéder à une remarquable approximation. Apollonius écrit un traité sur les coniques qui fascinent de nombreuses générations. Il y démontre les propriétés asymptotiques des hyperboles, des foyers et la base des propriétés des polaires réciproques.

L'antiquité n'est pas la seule période à utiliser des relations d'orthogonalité en géométrie. René Descartes généralise l'idée d'abscisses et d'ordonnées déjà présente chez Apollonius et utilise systématiquement l'angle droit pour définir ses repères, ce qui permet de calculer simplement la distance entre deux points dans le plan. Elle correspond à la somme des carrés des différences des coordonnées. Il utilise son repère pour établir les lois de l'optique comme celles de la réfraction et de le reflexion.

Isaac Newton utilise des propriétés d'orthogonalités (la traduction française utilise le mot perpendiculaire) pour établir les principes du calcul différentiel. Les définitions de dérivée et d'intégrale pour cet auteur se fonde sur des raisonnements géométriques où l'orthogonalité joue un rôle majeur. Newton les utilise pour déterminer la trajectoires des planètes autour du soleil. Son formalisme correspond essentiellement à une logique analogue à celle d'Euclide, le recours au repère cartésien est rare.