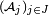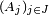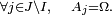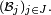Vendredi 2 Mai 2025
Rechercher 🔍

Indépendance (probabilités) - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - Indépendance de deux évènements - Indépendance des variables aléatoires - Indépendance de n évènements - Lemme de regroupement - Indépendance des tribus - Indépendance et information

Indépendance de n évènements

La notion d'indépendance peut être étendue à n événements, via la notion d'indépendance des tribus, mais on va plutôt donner ici deux critères plus lisibles :

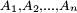
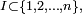
Critère 1 — n événements \scriptstyle\ A_1,A_2,\dots,A_n sont dits indépendants si et seulement si, pour toute partie \scriptstyle\ I\subset\{1,2,\dots,n\},\ on a

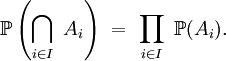
\mathbb{P}\left(\bigcap_{i\in I}\ A_i\right)\ =\ \prod_{i\in I}\ \mathbb{P}(A_i).

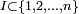
Le nombre total de conditions à vérifier est donc le nombre de parties \scriptstyle\ I\subset\{1,2,\dots,n\}\ possédant au moins deux éléments, à savoir :

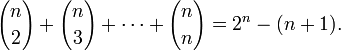
{n\choose 2} + {n\choose 3} + \cdots + {n\choose n} = 2^{n} - (n+1).

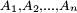
L'indépendance des n évènements \scriptstyle\ A_1,A_2,\dots,A_n entraîne que

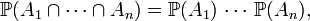
\mathbb{P}(A_1 \cap \cdots \cap A_n)=\mathbb{P}(A_1)\,\cdots\,\mathbb{P}(A_n),

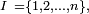
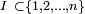
ce qui correspond au choix particulier \scriptstyle\ I\ =\{1,2,\dots,n\},\ mais est une propriété beaucoup plus faible que l'indépendance. Dans le même esprit, comme on le constate dans l'exemple ci-dessous, n événements peuvent être indépendants deux à deux, ce qui correspond à vérifier la propriété pour toutes les parties \scriptstyle\ I\ \subset\{1,2,\dots,n\}\ à 2 éléments, sans pour autant être indépendants :

Exemple  :

On lance deux dés et on pose

  • A1 : le résultat du lancer du dé n°1 est pair,
  • A2 : le résultat du lancer du dé n°2 est pair,
  • A3 : la somme des résultats des 2 lancers est impaire.

On a

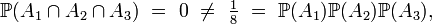
\mathbb{P}(A_1 \cap A_2 \cap A_3)\ =\ 0\ \neq\ \tfrac18\ =\ \mathbb{P}(A_1)\mathbb{P}(A_2)\mathbb{P}(A_3),

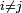
alors que, pourtant, pour \scriptstyle\ i\neq j\ choisis arbitrairement,

\mathbb{P}(A_i)=\mathbb{P}(A_j)=\tfrac12\quad\text{et}\quad\mathbb{P}(A_i\cap A_j)=\tfrac14.

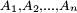
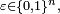
Critère 2 — n événements \scriptstyle\ A_1,A_2,\dots,A_n sont dits indépendants si et seulement si, pour tout choix de \scriptstyle\ \varepsilon\in\{0,1\}^n,\ on a

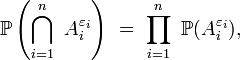
\mathbb{P}\left(\bigcap_{i= 1}^n\ A_i^{\varepsilon_i}\right)\ =\ \prod_{i=1}^n\ \mathbb{P}(A_i^{\varepsilon_i}),

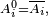
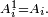
où, par convention, \scriptstyle\ A_i^0=\overline{A_i},\ et \scriptstyle\ A_i^1=A_i.\

Lemme de regroupement

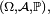
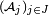
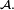
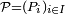
Lemme de regroupement — Dans un espace probabilisé \scriptstyle\ (\Omega,\mathcal{A},\mathbb{P}),\ soit une famille quelconque \scriptstyle\ (\mathcal{A}_{j})_{j\in J}\ de tribus indépendantes incluses dans \scriptstyle\ \mathcal{A}.\ Soit une partition \scriptstyle\ \mathcal{P}=(P_{i})_{i\in I}\ de \scriptstyle\ J.\ Notons

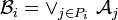
\mathcal{B}_i= \mathop{\vee}_{j\in P_i}\ \mathcal{A}_{j}

la tribu engendrée par

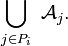
\bigcup_{j\in P_i}^{}\ \mathcal{A}_{j}.

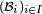
Alors la famille \scriptstyle\ (\mathcal{B}_{i})_{i\in I}\ est une famille de tribus indépendantes.

Applications  :

Le lemme de regroupement est utilisé, en probabilités, très souvent et de manière quasi-inconsciente. Citons quelques exemples :

  • l'inégalité de Kolmogorov ;
  • la propriété de Markov pour les processus de Galton-Watson ;
  • le principe de Maurey, ou méthode des différences bornées.

De manière plus élémentaire,

  • dans le cas fini, si (X1 , X2 , X3 , X4 , X5 ) est une famille de variables indépendantes, et si ƒ et g sont deux fonctions quelconques (mesurables), alors, par application du lemme de regroupement, ƒ(X2 , X3 , X5 ) et g(X1 , X4 ) sont deux variables indépendantes, car {2, 3, 5} et {1, 4} forment une partition de {1, 2, 3, 4, 5}.

Indépendance des tribus

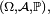
Définition — Dans un espace probabilisé \scriptstyle\ (\Omega,\mathcal{A},\mathbb{P}),\

  • une famille finie de tribus incluses dans \scriptstyle\ \mathcal{A}\ est une famille de tribus indépendantes si et seulement si
\forall (A_i)_{i\in I}\in\prod_{i\in I}\mathcal{A}_i,\qquad \mathbb{P}\left(\bigcap_{i\in I}A_i\right)=\ \prod_{i\in I}\ \mathbb{P}(A_i).
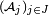
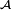
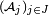
  • une famille quelconque \scriptstyle\ (\mathcal{A}_{j})_{j\in J}\ de tribus incluses dans \scriptstyle\ \mathcal{A}\ est une famille de tribus indépendantes si et seulement si toute sous famille finie de \scriptstyle\ (\mathcal{A}_{j})_{j\in J}\ est une famille de tribus indépendantes (c'est-à dire, si et seulement si, pour toute partie finie I de J, est une famille de tribus indépendantes).

Lien avec l'indépendance des évènements

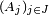
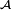
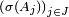
Définition —  Une famille \scriptstyle\ (A_{j})_{j\in J}\ d'évènements (i.e. d'éléments de \scriptstyle\ \mathcal{A}\ ) est une famille d'évènements indépendants si et seulement si \scriptstyle\ \left(\sigma(A_{j})\right)_{j\in J}\ est une famille de tribus indépendantes.

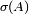
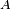
Comme la tribu \scriptstyle\ \sigma({A})\ engendrée par \scriptstyle\ A\ est décrite par :

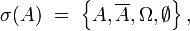
\sigma(A)\ =\ \left\{A,\overline{A},\Omega,\emptyset\right\},

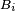
la définition donnée dans cette section pour une famille quelconque d'évènements, une fois particularisée à une famille de \scriptstyle\ n\ évènements, apparaît comme plus forte que les deux critères donnés plus haut. En effet, pour un choix approprié des évènements \scriptstyle\ B_i\ dans la définition

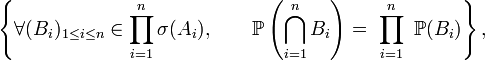
\left\{\forall (B_i)_{1\le i\le n}\in\prod_{i=1}^n\sigma({A}_i),\qquad \mathbb{P}\left(\bigcap_{i=1}^nB_i\right)=\ \prod_{i=1}^n\ \mathbb{P}(B_i)\right\},

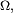
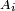
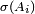
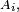
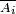
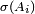
donnée dans cette section, on retrouve le critère 1 (choisir tantôt \scriptstyle\ \Omega,\ tantôt \scriptstyle\ A_i\ dans \scriptstyle\ \sigma({A}_i) ) et le critère 2 (choisir tantôt \scriptstyle\ A_i,\ tantôt \scriptstyle\ \overline{A_i}\ dans \scriptstyle\ \sigma({A}_i) ). Pourtant les critères 1 et 2 sont effectivement équivalents à la définition via les tribus, donnée dans cette section, mais cela mérite démonstration.

Lien avec l'indépendance des variables aléatoires

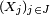
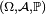
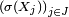
Définition —  Une famille \scriptstyle\ (X_{j})_{j\in J}\ de variables aléatoires définies sur \scriptstyle\ (\Omega,\mathcal{A},\mathbb{P})\ est une famille de variables aléatoires indépendantes si et seulement si \scriptstyle\ \left(\sigma(X_{j})\right)_{j\in J}\ est une famille de tribus indépendantes.

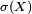
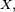
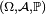
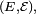
Comme la tribu \scriptstyle\ \sigma(X)\ engendrée une variable aléatoire \scriptstyle\ X,\ définie de \scriptstyle\ (\Omega,\mathcal{A},\mathbb{P})\ dans \scriptstyle\ (E,\mathcal{E}),\ est définie par :

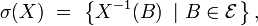
\sigma(X)\ =\ \left\{X^{-1}(B)\ \left|\ B\in\mathcal{E}\right.\right\},

la définition donnée dans cette section pour une famille quelconque de variables aléatoires, une fois particularisée à une famille de \scriptstyle\ n\ variables aléatoires, est clairement équivalente à la définition de la section Indépendance des variables aléatoires. En effet

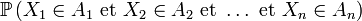
\mathbb{P}\left(X_1\in A_1\text{ et }X_2\in A_2\text{ et }\dots\text{ et }X_n\in A_n\right)

est un abus de notation pour

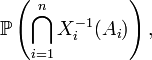
\mathbb{P}\left(\bigcap_{i=1}^nX_i^{-1}(A_i)\right),

et

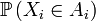
\mathbb{P}\left(X_i\in A_i\right)

est un abus de notation pour

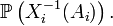
\mathbb{P}\left(X_i^{-1}(A_i)\right).

Propriétés élémentaires

Propriétés — 

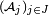
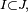
  • Une sous-famille d'une famille de tribus indépendantes est une famille de tribus indépendantes : si la famille \scriptstyle\ (\mathcal{A}_{j})_{j\in J}\ est une famille de tribus indépendantes et si \scriptstyle\ I\subset J,\ alors est une famille de tribus indépendantes .
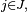
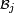
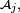
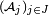
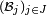
  • Si, pour tout \scriptstyle\ j\in J,\ la tribu \scriptstyle\ \mathcal{B}_{j}\ est incluse dans la tribu \scriptstyle\ \mathcal{A}_{j},\ et si la famille \scriptstyle\ (\mathcal{A}_{j})_{j\in J}\ est une famille de tribus indépendantes, alors la famille \scriptstyle\ (\mathcal{B}_{j})_{j\in J}\ est une famille de tribus indépendantes.

Pour démontrer le premier point on applique la définition de l'indépendance à la famille \scriptstyle\ (\mathcal{A}_{j})_{j\in J}\ en spécialisant à une famille \scriptstyle\ (A_{j})_{j\in J}\ d'évènements telle que \scriptstyle\ \forall j\in J\backslash I,\quad A_{j}=\Omega.\ Le second point est immédiat : il suffit d'écrire la définition de l'indépendance de la famille \scriptstyle\ (\mathcal{B}_{j})_{j\in J}.\

Indépendance des variables aléatoires
Indépendance et information
- Introduction - Indépendance de deux évènements - Indépendance des variables aléatoires - Indépendance de n évènements - Lemme de regroupement - Indépendance des tribus - Indépendance et information
miniature
Une éruption volcanique en 2018 responsable d'une explosion de vie 🌋
miniature
Un système d'exploitation pour les ordinateurs quantiques voit le jour 🖥️
miniature
Des singularités temporelles dans l'Univers ? 🕰️
miniature
Des fossiles de dinosaures mieux datés 🦖
miniature
Une gigantesque muraille de 10 milliards d'années-lumière dans l'Univers 🔭
miniature
Benchmark: les processeurs quantiques sous la loupe, quels sont les meilleurs ? 🏆
miniature
Découverte d'une "fourmi de l'enfer" vieille de 113 millions d'années 🐜
miniature
Le rôle méconnu de la décharge dans l'usure des batteries 🔋
miniature
1
La fonte des glaces déplace les pôles: quelles conséquences ? 🌍
miniature
L'appareil photo de votre smartphone peut détecter l'antimatière 📱
miniature
Cette étoile-zombie peut déformer les atomes à distance, et elle fonce dans notre galaxie ⭐
miniature
Un mosasaure géant découvert dans le Mississippi 🦕
miniature
Problème, les galaxies meurent plus tôt que prévu 🌀
miniature
Ce lien entre cannabis et troubles psychotiques 🧠
miniature
Une révolution dans le refroidissement des puces électroniques ? 🔥
miniature
Des parasites sous-marins filmés en train de vampiriser un poisson des abysses 👀
miniature
Lucy survole un astéroïde en forme de cacahuète 🚀
miniature
Découverte du fossile d'un dinosaure géant méconnu 🦕
miniature
Mars avait-elle un champ magnétique unilatéral ? 🔍
miniature
Des chimpanzés surpris à sociabiliser avec de l'alcool 🍇
miniature
Découverte macabre: ce gladiateur a été tué par un lion il y a 1 800 ans... en Grande-Bretagne 🦁
miniature
L'électroluminescence du graphène, une découverte inattendue ! 💡
miniature
Cet objet métallique n'a pas été fabriqué sur Terre 🔧
miniature
1
Cette innovation permet aux voitures électriques de charger 6 fois plus vite par grand froid ⚡
miniature
Cette super-Terre brûle les attentes des astronomes 🔥
miniature
Découverte exceptionnelle de fossiles d'amphibiens géants 🐸
miniature
Voici ce qui a causé les toutes premières inégalités de richesse 💰
miniature
Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊
miniature
Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭
miniature
Des cellules solaires flexibles battent des records d'efficacité ⚡
miniature
Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀
miniature
Record établi pour un transistor en diamant 💎
miniature
Les sursauts radio rapides trahissent enfin leur origine cosmique 📡
miniature
Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠
miniature
Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊
miniature
Les oscillations collectives des foules humaines denses 🔁
miniature
Une forme inconnue de la matière détectée au LHC ? ⚛️
miniature
Le sel, un facteur méconnu de l'obésité ? 🧂
miniature
L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀
miniature
Découverte tectonique majeure sous les Petites Antilles 🌍
miniature
1
Peut-on geler en chauffant ? ❄️
miniature
Une peau électronique pour doter les robots du sens du toucher 👌
miniature
Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳
miniature
Le cancer inscrit dans nos gènes dès la naissance ? 🧬
miniature
Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥
miniature
Le passé verdoyant du plus grand désert du monde 🐪
miniature
Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷
miniature
Des puces quantiques plus proches que jamais ⚡
miniature
1
Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬
miniature
En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊
Page générée en 0.160 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise