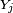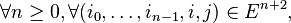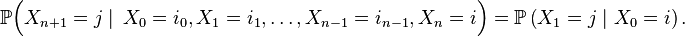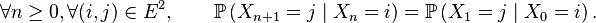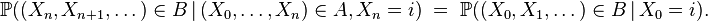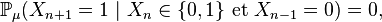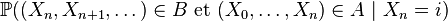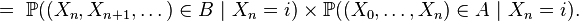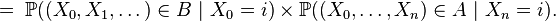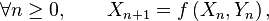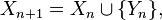Mercredi 2 Avril 2025
Rechercher 🔍

Propriété de Markov - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - Propriété de Markov faible (temps discret, espace discret) - Propriété de Markov faible (temps continu, espace discret) - Propriété de Markov forte (temps discret, espace discret) - Équation de Chapman-Kolmogorov-Smoluchowski

Introduction

En probabilité, un processus stochastique vérifie la propriété de Markov si et seulement si la distribution conditionnelle de probabilité des états futurs, étant donné les états passés et l'état présent, ne dépend en fait que de l'état présent et non pas des états passés (absence de « mémoire »). Un processus qui possède cette propriété est appelé processus de Markov. Pour de tels processus, la meilleure prévision qu'on puisse faire du futur, connaissant le passé et le présent, est identique à la meilleure prévision qu'on puisse faire du futur, connaissant uniquement le présent : si on connait le présent, la connaissance du passé n'apporte pas d'information supplémentaire utile pour la prédiction du futur.

Propriété de Markov faible (temps discret, espace discret)

Définition

C'est la propriété caractéristique d'une chaîne de Markov : en gros, la prédiction du futur à partir du présent n'est pas rendue plus précise par des éléments d'information supplémentaires concernant le passé, car toute l'information utile pour la prédiction du futur est contenue dans l'état présent du processus. 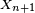La propriété de Markov faible possède plusieurs formes équivalentes qui reviennent toutes à constater que la loi conditionnelle de \scriptstyle\ X_{n+1}\ sachant le passé, i.e. 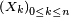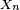sachant \scriptstyle\ \left(X_k\right)_{0\le k\le n}\ est une fonction de \scriptstyle\ X_n\ seul :

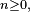
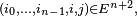
Propriété de Markov faible « élémentaire » —  Pour tout \scriptstyle\ n\ge 0,\ pour toute suite d'états \scriptstyle\ (i_0,\ldots,i_{n-1},i,j)\in E^{n+2},\

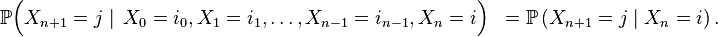
\begin{align}\mathbb{P}\Big(X_{n+1}=j&\mid\, X_0=i_0, X_1=i_1,\ldots, X_{n-1}=i_{n-1},X_n=i\Big) &= \mathbb{P}\left(X_{n+1}=j\mid X_n=i\right). \end{align}

On suppose le plus souvent les chaînes de Markov homogènes, i.e. on suppose que le mécanisme de transition ne change pas au cours du temps. La propriété de Markov faible prend alors la forme suivante :

\forall n\ge 0, \forall (i_0,\ldots,i_{n-1},i,j) \in E^{n+2},
\mathbb{P}\Big(X_{n+1}=j \mid\, X_0=i_0, X_1=i_1,\ldots, X_{n-1}=i_{n-1},X_n=i\Big) = \mathbb{P}\left(X_{1}=j\mid X_0=i\right).

Cette forme de la propriété de Markov faible est plus forte que la forme précédente, et entraîne en particulier que

\forall n\ge 0, \forall (i,j)\in E^{2},\qquad\mathbb{P}\left(X_{n+1}=j\mid X_n=i\right) = \mathbb{P}\left(X_{1}=j\mid X_0=i\right).

Dans la suite de l'article on ne considèrera que des chaînes de Markov homogènes. Pour une application intéressante des chaînes de Markov non homogènes à l'optimisation combinatoire, voir l'article Recuit simulé.

La propriété de Markov faible pour les chaînes de Markov homogènes a une autre forme, beaucoup plus générale que la précédente, mais pourtant équivalente à la précédente :

Propriété de Markov faible « générale » —  Pour n'importe quel choix de \scriptstyle\ n\ge 0,\quad B\in \mathcal P(E)^{\otimes{\mathbb N}},\quad A\in \mathcal P(E^{n+1}),\quad i\in E,

{\mathbb P}((X_{n}, X_{n+1}, \dots ) \in B\,|\,(X_0,\dots,X_{n}) \in A, X_n=i) \;=\;{\mathbb P}((X_{0}, X_{1}, \dots )\in B\,|\, X_0=i).

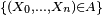
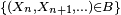
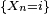
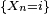
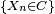
Notons que les évènements passés \scriptstyle\ \{(X_0,\dots,X_{n}) \in A\}\ et futurs \scriptstyle\ \{(X_{n}, X_{n+1}, \dots ) \in B\}\ prennent ici la forme la plus générale possible, alors que l'évènement présent \scriptstyle\ \{X_n=i\}\ reste sous une forme particulière, et pas par hasard : si on remplace \scriptstyle\ \{X_n=i\}\ par \scriptstyle\ \{X_n\in C\}\ dans l'énoncé ci-dessus, alors l'énoncé devient faux en général, car l'information sur le passé devient utile pour prévoir le présent (où \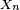scriptstyle\ X_n\ peut-il bien se trouver, plus précisément, à l'intérieur de la partie \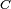scriptstyle\ C\  ?), et, partant de là, pour prévoir le futur.

Contrexemple de la marche aléatoire sur \scriptstyle\ \mathbb{Z}\  :

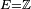
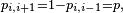
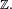
Si \scriptstyle\ E=\mathbb{Z}\ et \scriptstyle\ p_{i,i+1}=1-p_{i,i-1}=p,\ on parle de marche aléatoire sur \scriptstyle\ \mathbb{Z}.\ Supposons que \scriptstyle\ p\in]0,1[.\ Alors, par exemple,

\mathbb{P}_{\mu}(X_{n+1}=1\ |\ X_n\in\{0,1\}\text{ et }X_{n-1}=0)=0,\

alors qu'on peut facilement trouver \scriptstyle\ \mu\ et \scriptstyle\ n\ tels que

\mathbb{P}_{\mu}(X_{n+1}=1\ |\ X_n\in\{0,1\})>0.\

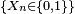
Ainsi, du fait d'une connaissance imprécise ( \scriptstyle\ \{X_n\in \{0,1\}\}\ ) du présent, certaines informations concernant le passé permettent d'améliorer le pronostic  : sachant que Xn-1 = 0, on en déduit que Xn n'est pas nul, donc que Xn est égal à 1, puis on conclut que Xn+1 ne peut être égal à 1. Par contre, sans l'information Xn-1 = 0, on ne peut exclure que Xn+1 soit égal à 1.

Pourtant, la marche aléatoire sur \scriptstyle\ \mathbb{Z}\ est une chaîne de Markov, et possède bien la propriété de Markov. Il n'y a pas de contradiction, ici : la propriété de Markov stipule que, lorsque l'on a une connaissance précise (Xn = i ) du présent, aucune information concernant le passé ne permet d'améliorer le pronostic.

Il existe une , liée à la notion de temps d'arrêt : cette propriété de Markov forte est cruciale pour la démonstration de résultats importants (divers critères de récurrence, loi forte des grands nombres pour les chaînes de Markov).

Indépendance conditionnelle

La propriété de Markov faible « générale » entraine que

Indépendance conditionnelle —  Pour n'importe quel choix de \scriptstyle\ n\ge 0,\quad B\in \mathcal P(E)^{\otimes{\mathbb N}},\quad A\in \mathcal P(E^{n+1}),\quad i\in E,

{\mathbb P}((X_{n}, X_{n+1}, \dots ) \in B\text{ et } (X_0,\dots,X_{n}) \in A\ |\ X_n=i)
=\;{\mathbb P}((X_{n}, X_{n+1}, \dots ) \in B\ |\ X_n=i)\times{\mathbb P}((X_0,\dots,X_{n}) \in A\ |\ X_n=i).

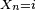
Cette égalité exprime l'indépendance conditionnelle entre le passé et le futur, sachant le présent (sachant que \scriptstyle\ X_n=i\ ). Cependant, si l'on compare avec la propriété de Markov faible « générale » telle qu'énoncée plus haut, on constate qu'on a perdu la propriété d'homogénéité : la propriété de Markov faible « générale » est en fait équivalente à la propriété plus forte

Indépendance conditionnelle et homogénéité —  Pour n'importe quel choix de \scriptstyle\ n\ge 0,\quad B\in \mathcal P(E)^{\otimes{\mathbb N}},\quad A\in \mathcal P(E^{n+1}),\quad i\in E,

{\mathbb P}((X_{n}, X_{n+1}, \dots ) \in B\text{ et } (X_0,\dots,X_{n}) \in A\ |\ X_n=i)
=\; {\mathbb P}((X_{0}, X_{1}, \dots )\in B\ |\ X_0=i)\times{\mathbb P}((X_0,\dots,X_{n}) \in A\ |\ X_n=i).

Critère

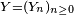
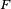
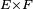
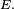
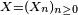
Critère fondamental — Soit une suite \scriptstyle\ Y=(Y_{n})_{n\ge 0}\ de variables aléatoires indépendantes et de même loi, à valeurs dans un espace \scriptstyle\ F\ , et soit \scriptstyle\ f\ une application mesurable de \scriptstyle\ E\times F\ dans \scriptstyle\ E.\ Supposons que la suite \scriptstyle\ X=(X_{n})_{n\ge 0}\ est définie par la relation de récurrence :

\forall n\ge 0,\qquad X_{n+1}=f\left(X_n,Y_{n}\right),

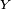
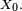
et supposons que la suite \scriptstyle\ Y\ est indépendante de \scriptstyle\ X_0.\ Alors \scriptstyle\ X\ est une chaîne de Markov homogène.

Collectionneur de vignettes (coupon collector)  :

Petit Pierre fait la collection des portraits des onze joueurs de l'équipe nationale de football, qu'il trouve sur des vignettes à l'intérieur de l'emballage des tablettes de chocolat Cémoi ; chaque fois qu'il achète une tablette il a une chance sur 11 de tomber sur le portrait du joueur n° \scriptstyle\ k\ (pour tout \scriptstyle\ k\ ). On note \scriptstyle\ X_{n}\in\mathcal{P}([\![ 1,11]\!])\ l'état de la collection de Petit Pierre, après avoir ouvert l'emballage de sa \scriptstyle\ n\ -ème tablette de chocolat. 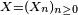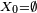\scriptstyle\ X=(X_{n})_{n\ge 0}\ est une chaîne de Markov partant de \scriptstyle\ X_{0}=\emptyset\ , car elle rentre dans le cadre précédent pour le choix \scriptstyle\ F=[\![1,11]\!],\ E=\mathcal{P}(F),\ f(x,y)=x\cup\{y\},\ puisque

X_{n+1}=X_n\cup\{Y_n\},

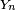
où les variables aléatoires \scriptstyle\ Y_{n}\ sont des variables aléatoires indépendantes et uniformes sur \scriptstyle\ [\![1,11]\!]\  : ce sont les numéros successifs des vignettes tirées des tablettes de chocolat. 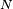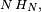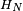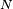Le temps moyen nécessaire pour compléter la collection (ici le nombre de tablettes que Petit Pierre doit acheter en moyenne pour compléter sa collec') est, pour une collection de \scriptstyle\ N\ vignettes au total, de \scriptstyle\ N\,H_N,\ où \scriptstyle\ H_N\ est le \scriptstyle\ N\ -ème nombre harmonique. 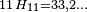Par exemple, \scriptstyle\ 11\,H_{11}=33,2\dots\quad tablettes de chocolat.

Remarques  :
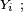
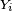
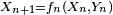
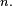
  • La propriété de Markov découle de l'indépendance des \scriptstyle\ Y_i\ ;\ elle reste vraie lorsque les \scriptstyle\ Y_i\ ont des lois différentes, et lorsque la « relation de récurrence » \scriptstyle\ X_{n+1}=f_n\left(X_n,Y_{n}\right)\ dépend de \scriptstyle\ n.\ Les hypothèses faites en sus de l'indépendance sont là uniquement pour assurer l'homogénéité de la chaîne de Markov.
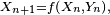
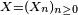
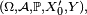
  • Le critère est fondamental en cela que toute chaîne de Markov homogène peut être simulée exactement via une récurrence de la forme \scriptstyle\ X_{n+1}=f\left(X_n,Y_{n}\right),\ pour une fonction \scriptstyle\ f\ bien choisie. 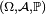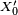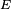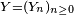Plus précisément, si \scriptstyle\ X=(X_{n})_{n\ge 0}\ est une chaîne de Markov homogène, il existe un quintuplet \scriptstyle\ (\Omega,\mathcal{A},\mathbb{P},X^{\prime}_0,Y),\ où \scriptstyle\ (\Omega,\mathcal{A},\mathbb{P})\ désigne un espace de probabilité, \scriptstyle\ X^{\prime}_0\ est une variable aléatoire à valeurs dans \scriptstyle\ E\ et où \scriptstyle\ Y=(Y_{n})_{n\ge 0}\ est une suite de variables aléatoires i.i.d. 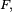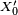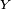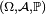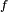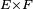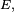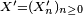à valeurs dans \scriptstyle\ F,\ \ \scriptstyle\ X^{\prime}_0\ et \scriptstyle\ Y\ étant définies sur \scriptstyle\ (\Omega,\mathcal{A},\mathbb{P})\ et indépendantes, et il existe une application \scriptstyle\ f\ \ définie de \scriptstyle\ E\times F\ dans \scriptstyle\ E,\ telles que la suite \scriptstyle\ X^{\prime}=(X^{\prime}_{n})_{n\ge 0}\ définie par
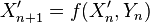
X^{\prime}_{n+1}=f(X^{\prime}_n,Y_n)
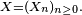
ait même loi que la suite \scriptstyle\ X=(X_{n})_{n\ge 0}.\
  • On peut même choisir \scriptstyle\ F=[0,1],\ et choisir des variables \scriptstyle\ Y_{j}\ indépendantes et uniformes sur l'intervalle [0,1], ce qui est commode pour l'étude de chaînes de Markov via des méthodes de Monte-Carlo, i.e. par simulation de trajectoires « typiques » de chaînes de Markov.
Propriété de Markov faible (temps continu, espace discret)
- Introduction - Propriété de Markov faible (temps discret, espace discret) - Propriété de Markov faible (temps continu, espace discret) - Propriété de Markov forte (temps discret, espace discret) - Équation de Chapman-Kolmogorov-Smoluchowski
miniature
Les océans de la Terre n'avaient autrefois pas du tout la même couleur 🌊
miniature
Une cartographie inédite révèle la consommation énergétique du cerveau 🧠
miniature
Des chercheurs ont intercepté et décodé "facilement" des messages sous-marins depuis les airs ✈️
miniature
Voici pourquoi les femmes ressentent plus de douleur chronique que les hommes 🧐
miniature
Un immense iceberg se détache et révèle ce surprenant écosystème caché depuis des siècles 🦑
miniature
Un colibri imite une chenille pour survivre: découvrez cette stratégie étonnante 🐦
miniature
Cette forme de vie géante ne ressemble à rien d'autre de connu 🌎
miniature
Recherche: cette nouvelle molécule se montre terriblement efficace contre la calvitie 🔬
miniature
1
Des tardigrades génétiquement modifiés pour survivre... sur le Soleil ☀️
miniature
Or, cuivre... pourquoi ces métaux précieux se trouvent dans les zones de subduction ? 🌋
miniature
Une avancée majeure dans la supraconductivité à haute température 🌡️
miniature
Les chimpanzés fabriquent leurs outils comme des ingénieurs 🛠️
miniature
Mach 16: des surprises physiques découvertes dans les vols hypersoniques 🚀
miniature
Des scientifiques ont réussi à filmer la séparation des brins de l'ADN 🧬
miniature
Comment 13 degrés peuvent transformer une foule en chaos ? 🚶‍♂️
miniature
Découverte: les phoques savent évaluer la quantité d'oxygène dans leur sang 🤿
miniature
Les trous noirs pourraient-ils protéger la vie dans l'Univers ? 🌱
miniature
Implants mammaires en silicone: une toxicité remise en question
miniature
Découverte d'un "broyeur d'étoiles" dans notre galaxie 🌀
miniature
Neandertal et Sapiens: une collaboration inattendue il y a 100 000 ans 🤝
miniature
Que sont ces sphères noires découvertes sur Mars ? 🔴
miniature
Découverte: les champignons contre... la grippe 🍄
miniature
Découverte inédite: voici comment notre cerveau attache les souvenirs entre eux 🖇️
miniature
Découverte: les requins émettent des sons ! 🦈
miniature
Des scientifiques inventent un ciment qui aspire le CO2 🌎
miniature
Comment le cerveau décode le temps: du récit aux réseaux neuronaux 🕰️
miniature
Horloge atomique dans son smartphone et GPS 1000 fois plus précis ⏱️
miniature
L'ocytocine: l'hormone de l'amour ou simple mythe ? 💕
miniature
Cette nouvelle méthode permettrait d'identifier une vie extraterrestre inattendue 👽
miniature
Une araignée géante filmée dans les abysses de l'Antarctique 🕷️
miniature
Trois familles d'objets planétaires identifiées dans le Système Solaire externe 🔭
miniature
Découverte d'une griffe géante à 2 doigts appartenant à une nouvelle espèce de dinosaure 🦖
miniature
Un nouvelle technologie de vaisseaux nucléaires pour explorer le Système solaire 🚀
miniature
Votre cerveau se consomme lui-même pour rechercher de l'énergie, pendant un exercice intense 🏃
miniature
Des vestiges organiques découverts sur Mars 🧐
miniature
Pourquoi les armes nucléaires sont-elles si difficiles et dangereuses à produire ? 💥
miniature
MRAM: la mémoire informatique du futur enfin là ? ⚡
miniature
Vidange d'un lac glaciaire: la catastrophe du Sikkim en 2023 expliquée 🌊
miniature
1
Qu'est-ce qui a bien pu creuser ces tunnels il y a plusieurs millions d'années ? ⛏️
miniature
Les secrets biologiques de Maria Branyas Morera, la supercentenaire 🕰️
miniature
Exploiter la rotation terrestre pour produire de l'électricité: l'énergie verte de demain ? ⚡
miniature
Que nous apprennent ces émissions radioactives de météorites lunaires et martiennes ? ☢️
miniature
La Chine dévoile un processeur quantique fiable à 99.9% 🚀
miniature
Voici les emblématiques espèces éteintes que la science pourrait bientôt ressusciter 🦣
miniature
Un poisson de 15 millions d'années incroyablement préservé 🐟
miniature
Existence démontrée d'un lien entre muscles, cerveau et fertilité 💪
miniature
Prévision météo: une petite IA surclasse les plus gros supercalculateurs 🌤️
miniature
Cette fosse commune révèle une histoire de violence extrême et de respect ⚔️
miniature
Cette nouvelle cellule solaire dure 10 fois plus longtemps 🌞
miniature
Des poulets aux plumes de dinosaures: une expérience génétique étonnante 🐔
Page générée en 0.155 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise