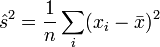Jackknife - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Exemple
Pour n=25 tirages indépendants dans la loi bêta de paramétres (3;7), on considère l'estimateur (biaisé) de la variance :
| 0,21876 | 0,11996 | 0,25072 | 0,30178 | 0,14852 |
| 0,16383 | 0,14686 | 0,29925 | 0,15777 | 0,45958 |
| 0,41439 | 0,45365 | 0,41157 | 0,29788 | 0,30316 |
| 0,25900 | 0,69559 | 0,14129 | 0,12868 | 0,14144 |
| 0,32000 | 0,30767 | 0,30478 | 0,28287 | 0,14855 |
Sur l'échantillon, cet estimateur vaut 0,017892 pour une vraie valeur de 0,01909091. L'estimateur par la méthode jackknife vaut quant à lui 0,01863750 : le biais, même en petit échantillon, a été réduit. On peut construire un intervalle de confiance à 95 % : la variance de l'estimateur est 5,240744e-05 ce qui donne un intervalle de [0,003696325;0,033578679] qui contient la vraie valeur.