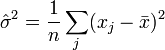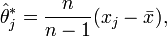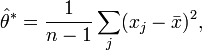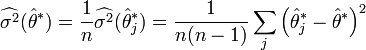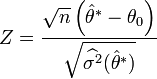Jackknife - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En statistiques, le jackknife ((en) couteau suisse) est une méthode de rééchantillonnage qui tire son nom de couteau suisse du fait qu'elle peut être utile à diverses choses : réduction du biais en petit échantillon, construction d'un intervalle de confiance raisonnable pour toute sorte de statistiques, test statistique. À partir des années 70, cette méthode de rééchantillonnage a été "remplacée" par une méthode plus sophistiquée, le bootstrap.
Exposé général
Le cas de la moyenne empirique
On dispose d'un échantillon
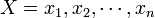
Un estimateur naturel est la moyenne empirique :
-
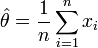
Un moyen de mesurer l'impact d'une observation xj sur l'estimateur
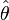
On remarque que
et en passant à la moyenne que
où
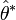
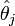
Ainsi, on a
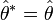
Généralisation
Dans l'exposé précédent, la méthode du jackknife n'apporte rien dans le sens où il est confondu avec l'estimateur naturel. La généralisation montre qu'il en va tout autrement lorsqu'on considère un paramètre quelconque
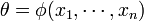
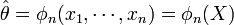
Comme précédemment, on considère l'estimation de θ sur l'échantillon privé de sa je observation X − j :
ce qui permet de poser
comme étant la je pseudo-valeur.
Ces estimations partielles peuvent être vues comme des variables indépendantes et d'espérance θ. On peut alors définir l'estimateur jackknife de θ en prenant la moyenne empirique :
On peut généraliser cette approche en considérant un échantillon amputé non plus d'une seule observations, mais de plusieurs. Le point cléf reste la définition des pseudo valeurs
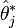
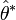
Réduction du biais
- Principe général
Quenouille a montré en 1949 que l'estimateur jackknife permet de réduire le biais de l'estimation initiale
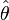
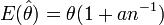
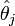
L'élément clef est la transposition de
en
puis en développant
ce qui a permis d'ôter le biais du premier ordre. On pourrait itérer pour ôter les biais d'ordre supérieur.
- Exemple (estimation sans biais de la variance)
Considérons l'estimateur de la variance :
Il est bien connu que cet estimateur est biaisé. En considérant les pseudo-valeurs, on a :
puis on en déduit que :
ce qui est l'estimateur non-biaisé de la variance. Nous venons de résorber le biais.
Intervalle de confiance
Un autre utilisation de la méthode jackknife, due à Turkey en 1958, est de fournir un intervalle de confiance pour l'estimateur
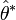
On peut ainsi construire comme intervalle de confiance approximatif au seuil 1 − α :
où tα / 2;n − 1 est le quantile approprié d'une loi de Student.
Test statistique
Le bootstrap peut aussi servir à tester une hypothèse
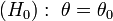
à une loi normale standard.
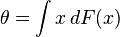
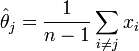
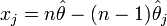
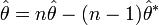
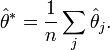
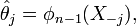
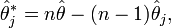
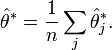
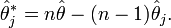
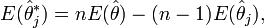
![E(\hat\theta_j^\ast) = \theta\left[n\left(1+\frac{a}{n} \right) -(n-1)\left(1+\frac{a}{n-1} \right)\right] = \theta,](https://static.techno-science.net/illustration/Definitions/autres/0/0cf69ef619457302c951193f0ba50b1a_946df421af3143b84b2640c1d7421be4.png)