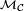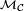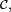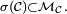Lemme de classe monotone - Définition
La liste des auteurs de cet article est disponible ici.
Énoncé et démonstration du lemme de classe monotone
Lemme de classe monotone — La plus petite classe monotone contenant le π-système

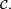
On note
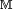
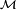
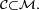
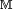
-
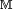
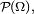
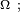
- ainsi l'intersection
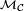
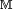
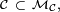
- par ailleurs, l'intersection de n'importe quelle famille de classes monotones est encore une classe monotone, donc
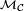
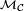
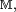
- enfin
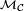
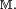
La classe
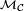
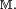
On note
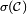
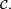
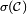
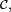
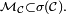
Dans la suite de la démonstration, on s'attache à montrer que
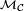
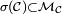
Proposition — Une classe monotone qui est de plus stable par intersection est alors une tribu.
En effet toute classe monotone
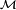
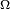
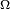
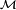
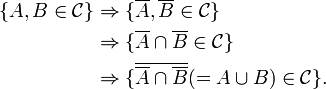
Par une récurrence évidente, la réunion d'une famille finie d'éléments de
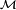
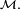
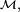
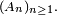
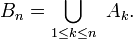
Alors
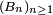
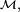
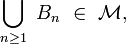
mais par ailleurs, on peut démontrer, par exemple par double inclusion, que
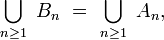
La proposition est donc démontrée.
Il ne nous reste plus qu'à montrer que
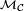
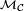
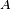
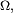
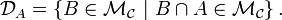
On montre facilement, d'une part que
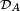
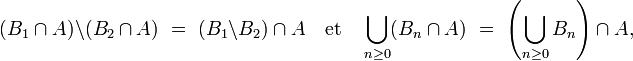
d'autre part que si
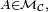
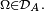
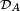
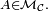
- si
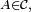

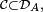
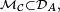
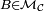
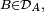
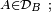
- ainsi, pour un élément
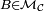
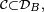
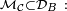

Par application de la Proposition,