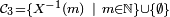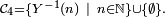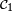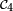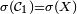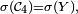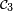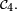Vendredi 13 Décembre 2024
Rechercher 🔍

Lemme de classe monotone - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - Classe monotone et π-système - Applications - Énoncé et démonstration du lemme de classe monotone

Introduction

Triangle de Sierpiński
Carré de Sierpiński

Le lemme de classe monotone, dû à Wacław Sierpiński et popularisé par Dynkin, permet de démontrer, de manière économique, l'égalité entre deux lois de probabilité : de même que deux applications linéaires qui coïncident sur une base coïncident sur l'espace entier, deux mesures de probabilité qui coïncident sur un π-système, coïncident sur la tribu engendrée par ce π-système.

Dans certains ouvrages, le lemme de classe monotone apparaît sous le nom de « Théorème pi-lambda de Dynkin ».

Classe monotone et π-système

Définition — 

  • Une classe \scriptstyle\ \mathcal{C}\ de parties d'un ensemble Ω est appelé π-système si cette classe est stable par intersection finie :
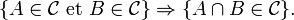
\{A\in \mathcal{C}\text{ et }B\in \mathcal{C}\}\Rightarrow\{A\cap B\in \mathcal{C}\}.
  • Une classe \scriptstyle\ \mathcal{M}\ de parties d'un ensemble Ω est appelé λ-système ou classe monotone si cette classe contient Ω et est stable par différence, et par réunion croissante :
\begin{align} \{A\in \mathcal{M}\text{ et }B\in \mathcal{M}\text{ et }A\subset B\}\quad&\Rightarrow\quad\{B\backslash A\in \mathcal{M}\}, \\ \{\forall n\ge 0,\quad \{A_{n}\in \mathcal M\text{ et } A_{n}\subset A_{n+1}\}\}\quad&\Rightarrow\quad\left\{\bigcup_{n\ge 0} A_{n}\ \in \mathcal M\right\}.\end{align}
Exemples de π-systèmes  :
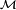
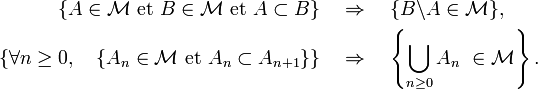
  • une classe d'intervalles : \scriptstyle\ \mathcal{C}_1=\{]-\infty,\,x]\ |\ x\in\R\}.
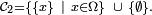
  • la classe des singletons : \scriptstyle\ \mathcal{C}_2=\{\{x\}\ |\ x\in \Omega\}\ \cup\ \{\emptyset\}.
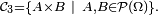
  • la classe des pavés : \scriptstyle\ \mathcal{C}_3=\{A\times B\ |\ A,B\in \mathcal{P}(\Omega)\}.
Un exemple de classe monotone  :

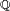
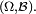
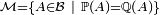
Soit deux mesures de probabilité \scriptstyle\ \mathbb{P}\ et \scriptstyle\ \mathbb{Q}\ définies sur \scriptstyle\ (\Omega,\mathcal{B}).\ La classe \scriptstyle\ \mathcal{M}=\{A\in\mathcal{B}\ |\ \mathbb{P}(A)=\mathbb{Q}(A)\}\ est une classe monotone.

Applications

Lemme d'unicité des mesures de probabilité

Le lemme de classe monotone a une conséquence immédiate

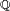
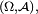
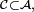
Lemme d'unicité des mesures de probabilité —  Deux mesures de probabilité \scriptstyle\ \mathbb{P}\ et \scriptstyle\ \mathbb{Q}\ définies sur l'espace probabilisable \scriptstyle\ (\Omega,\mathcal{A}),\ et coincidant sur le π-système \scriptstyle\ \mathcal{C}\subset \mathcal{A},\ concident aussi sur la tribu engendrée par \scriptstyle\ \mathcal{C}\  :

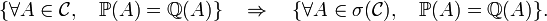
\{\forall A\in \mathcal{C},\quad \mathbb{P}(A)=\mathbb{Q}(A)\}\quad\Rightarrow\quad\{\forall A\in \sigma(\mathcal{C}),\quad \mathbb{P}(A)=\mathbb{Q}(A)\}.

On pose

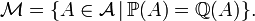
\mathcal{M}=\{A\in \mathcal{A}\,|\, \mathbb{P}(A)=\mathbb{Q}(A)\}.

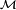
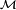
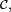
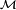
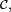
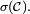
On vérifie facilement que \scriptstyle\ \mathcal{M}\ est une classe monotone. Comme \scriptstyle\ \mathcal{M}\ est une classe monotone contenant \scriptstyle\ \mathcal{C},\ \scriptstyle\ \mathcal{M}\ contient la plus petite classe monotone contenant \scriptstyle\ \mathcal{C},\ à savoir \scriptstyle\ \sigma(\mathcal{C}).\

Parmi de nombreuses applications importantes du lemme d'unicité, citons celle qui est peut-être la plus importante :

Corollaire — Il suit que :

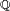
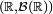
  • deux mesures de probabilité \scriptstyle\ \mathbb{P}\ et \scriptstyle\ \mathbb{Q}\ définies sur \scriptstyle\ (\R,\mathcal{B}(\R))\ sont égales si elles ont même fonction de répartition ;
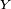
  • deux variables aléatoires réelles \scriptstyle\ X\ et \scriptstyle\ Y\ ont même loi si elles ont même fonction de répartition.

On pose

\mathcal{C}=\{]-\infty,\,x]\,|\, x\in\R\}.

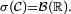
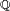
La classe \scriptstyle\ \mathcal{C}\ est un π-système, et \scriptstyle\ \sigma(\mathcal{C})=\mathcal{B}(\R).\ Comme les deux mesures de probabilité \scriptstyle\ \mathbb{P}\ et \scriptstyle\ \mathbb{Q}\ ont même fonction de répartition, i.e.

\forall x\in\R,\qquad \mathbb{P}(]-\infty,\,x])=\mathbb{Q}(]-\infty,\,x]),

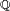
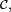
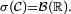
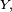
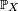
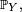
\scriptstyle\ \mathbb{P}\ et \scriptstyle\ \mathbb{Q}\ coïncident sur \scriptstyle\ \mathcal{C},\ donc sur \scriptstyle\ \sigma(\mathcal{C})=\mathcal{B}(\R).\ Par définition, deux variables aléatoires réelles, \scriptstyle\ X\ et \scriptstyle\ Y,\ ont même fonction de répartition si leurs lois de probabilité, \scriptstyle\ \mathbb{P}_X\ et \scriptstyle\ \mathbb{P}_Y,\ ont même fonction de répartition :

\forall A\in\mathcal{B}(\R),\quad \mathbb{P}_X(A)=\mathbb{P}(X\in A),\qquad\text{et }\forall x\in\R,\quad \mathbb{P}_X(]-\infty,\,x])=\mathbb{P}(X\le x).

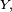
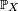
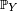
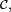
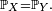
Ainsi, si \scriptstyle\ X\ et \scriptstyle\ Y,\ ont même fonction de répartition, \scriptstyle\ \mathbb{P}_X\ et \scriptstyle\ \mathbb{P}_Y\ coïncident sur \scriptstyle\ \mathcal{C},\ donc \scriptstyle\ \mathbb{P}_X=\mathbb{P}_Y.\

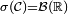
Expliquons brièvement pourquoi \scriptstyle\ \sigma(\mathcal{C})=\mathcal{B}(\R)\  :

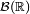
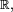
  • \scriptstyle\ \mathcal{B}(\R)\ est par définition la tribu engendrée par les ouverts de \scriptstyle\ \R,\
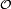
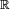
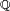
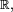
  • un ouvert \scriptstyle\ \mathcal{O}\ de \scriptstyle\ \R\ est réunion dénombrable d'intervalles ouverts, car, par densité de \scriptstyle\ \Q\ dans \scriptstyle\ \R,\ on a
\mathcal{O}=\bigcup_{(a,b)\in E}]a,b[,\qquad\text{avec}\qquad E=\{(a,b)\in\Q^2\,|\,a<b,\ ]a,b[\subset\mathcal{O}\},
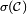
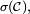
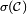
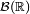
  • et les intervalles ouverts appartiennent à \scriptstyle\ \sigma(\mathcal{C})\ (donc les ouverts appartiennent à \scriptstyle\ \sigma(\mathcal{C}),\ donc \scriptstyle\ \sigma(\mathcal{C})\ contient \scriptstyle\ \mathcal{B}(\R)\ ), car
]a,b[=]-\infty,a]^c\,\cap\,\left(\bigcup_{n\ge 1}]-\infty,b-\tfrac1n]\right).

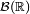
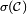
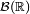
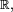
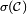
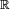
Pour l'inclusion en sens inverse ( \scriptstyle\ \mathcal{B}(\R)\ contient \scriptstyle\ \sigma(\mathcal{C})\ ), notons que \scriptstyle\ \mathcal{B}(\R)\ est la tribu engendrée par tous les fermés de \scriptstyle\ \R,\ alors que \scriptstyle\ \sigma(\mathcal{C})\ est engendrée par certains fermés de \scriptstyle\ \R\ seulement.

Critères d'indépendance

Par exemple,

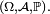
Critères — Soit X et Y deux variables aléatoires réelles définies sur un espace probabilisé \scriptstyle\ (\Omega,\mathcal{A},\mathbb{P}).\

  • Si, pour tout couple (x,y) de nombres réels,
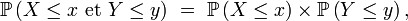
\mathbb{P}\left(X\le x\text{ et }Y\le y\right)\ =\ \mathbb{P}\left(X\le x\right)\times\mathbb{P}\left(Y\le y\right),
alors X et Y sont indépendantes.
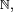
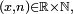
  • Si Y est à valeurs dans \scriptstyle\ \mathbb{N},\ et si, pour tout couple \scriptstyle\ (x,n)\in\mathbb{R}\times\mathbb{N},\
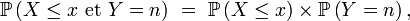
\mathbb{P}\left(X\le x\text{ et }Y=n\right)\ =\ \mathbb{P}\left(X\le x\right)\times\mathbb{P}\left(Y=n\right),
alors X et Y sont indépendantes.
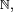
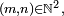
  • Bien sûr, si X et Y sont à valeurs dans \scriptstyle\ \mathbb{N},\ et si, pour tout couple \scriptstyle\ (m,n)\in\mathbb{N}^2,\
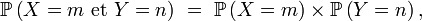
\mathbb{P}\left(X=m\text{ et }Y=n\right)\ =\ \mathbb{P}\left(X=m\right)\times\mathbb{P}\left(Y=n\right),
alors X et Y sont indépendantes.

La démonstration du dernier critère ne nécessite pas le lemme de classe monotone, mais ce lemme est très utile pour la démonstration des deux premiers critères. On peut utiliser le deuxième critère pour démontrer, par exemple, que dans la méthode de rejet, le nombre d'itérations est indépendant de l'objet aléatoire (souvent un nombre aléatoire) engendré au terme de ces itérations. Pour la démonstration de ces critères, ainsi que pour la démonstration du lemme de regroupement, on a besoin de la définition et de la proposition suivantes.

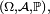
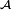
Définition — Dans un espace probabilisé \scriptstyle\ (\Omega,\mathcal{A},\mathbb{P}),\ une famille finie de classes incluses dans \scriptstyle\ \mathcal{A}\ est une famille indépendante si et seulement si

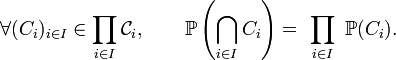
\forall (C_i)_{i\in I}\in\prod_{i\in I}\mathcal{C}_i,\qquad \mathbb{P}\left(\bigcap_{i\in I}C_i\right)=\ \prod_{i\in I}\ \mathbb{P}(C_i).

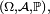
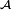
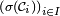
Proposition — Si, dans un espace probabilisé \scriptstyle\ (\Omega,\mathcal{A},\mathbb{P}),\ une famille finie de π-systèmes inclus dans \scriptstyle\ \mathcal{A}\ est une famille indépendante, alors la famille \scriptstyle\ \left(\sigma(\mathcal{C}_{i})\right)_{i\in I}\ est une famille de tribus indépendantes.

On pose

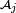
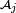
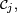
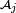
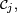
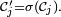
On vérifie facilement que \scriptstyle\ \mathcal{A}_j\ est une classe monotone. 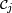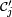Comme \scriptstyle\ \mathcal{A}_j\ est une classe monotone contenant \scriptstyle\ \mathcal{C}_j,\ \scriptstyle\ \mathcal{A}_j\ contient la plus petite classe monotone contenant \scriptstyle\ \mathcal{C}_j,\ à savoir \scriptstyle\ \mathcal{C}^{\prime}_j=\sigma(\mathcal{C}_j).\ La nouvelle famille de π-systèmes obtenue en remplaçant \scriptstyle\ \mathcal{C}_j\ par \scriptstyle\ \mathcal{C}^{\prime}_j\ dans la famille est donc encore une famille de π-systèmes indépendants. 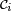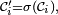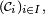On peut par le même raisonnement remplacer successivement chaque \scriptstyle\ \mathcal{C}_i\ par \scriptstyle\ \mathcal{C}^{\prime}_i=\sigma(\mathcal{C}_i),\ dans la famille \scriptstyle\ (\mathcal{C}_{i})_{i\in I},\ sans que cette famille perde sa propriété d'indépendance. 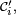Notons qu'une tribu, et en particulier chaque \scriptstyle\ \mathcal{C}^{\prime}_i,\ est aussi, nécessairement, un π-système.

Applications  :
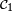
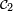
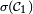
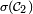
  • Posons \scriptstyle\ \mathcal{C}_1=\{X^{-1}(]-\infty,\,x])\ |\ x\in\R\} et \scriptstyle\ \mathcal{C}_2=\{Y^{-1}(]-\infty,\,y])\ |\ y\in\R\}. Alors, sous les hypothèses du premier critère, \scriptstyle\ \mathcal{C}_1 et \scriptstyle\ \mathcal{C}_2 sont des π-systèmes indépendants. En vertu de la proposition, \scriptstyle\ \sigma(\mathcal{C}_1) et \scriptstyle\ \sigma(\mathcal{C}_2) sont alors des tribus indépendantes. 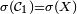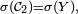Mais \scriptstyle\ \sigma(\mathcal{C}_1)=\sigma(X) et \scriptstyle\ \sigma(\mathcal{C}_2)=\sigma(Y), ce qui assure bien l'indépendance du couple (X,Y).
  • Posons \scriptstyle\ \mathcal{C}_3=\{X^{-1}(m)\ |\ m\in\N\}\cup\{\emptyset\} et \scriptstyle\ \mathcal{C}_4=\{Y^{-1}(n)\ |\ n\in\N\}\cup\{\emptyset\}. Sous les hypothèses du deuxième critère, \scriptstyle\ \mathcal{C}_1 et \scriptstyle\ \mathcal{C}_4 sont des π-systèmes indépendants. Par ailleurs, \scriptstyle\ \sigma(\mathcal{C}_1)=\sigma(X) et \scriptstyle\ \sigma(\mathcal{C}_4)=\sigma(Y), et on conclut comme précédemment. Pour démontrer le troisième critère, on utilise cette fois \scriptstyle\ \mathcal{C}_3 et \scriptstyle\ \mathcal{C}_4.
Énoncé et démonstration du lemme de classe monotone
- Introduction - Classe monotone et π-système - Applications - Énoncé et démonstration du lemme de classe monotone
miniature
Une nouvelle manière de lire les mémoires magnétiques 🧲
miniature
1
Vous êtes né avant 1986 ? Voici pourquoi vous risquez de développer des troubles psychiques ⚠️
miniature
Ce nouveau modèle relie matière noire et inflation cosmique 🌀
miniature
Ils ont rendu ce bois bioluminescent: vers un nouveau mode d'éclairage ? 💡
miniature
Des mouches dans la station spatiale chinoise Tiangong 🛰️
miniature
Cette main-robot nanométrique est capable de saisir des virus (exemple avec la COVID-19) 🖐️
miniature
1
Une étoile dévorée à pleine vitesse par... un trou noir ? 🌟
miniature
Cette astuce simple réduit la consommation d'alcool... des femmes 🍷
miniature
Découverte: la lumière transforme un isolant en métal 💡
miniature
Cet aliment à bannir nourrit les cancers 🍽️
miniature
Cette tablette de 3000 ans dévoile une écriture jusqu'alors inconnue ✍️
miniature
Découverte d'une chimie des océans refroidissant le climat 🌊
miniature
Le télescope James Webb, poussé à ses limites, découvre ces structures incroyablement anciennes 🔭
miniature
Le rôle surprenant de la grossesse contre la grippe A 🦠
miniature
Découverte d'une nouvelle espèce éteinte grâce à... un accélérateur de particules ⚛️
miniature
Une avancée prometteuse pour le déploiement des batteries sodium-ion 🔋
miniature
Voici comment et pourquoi le risque de cancer augmente... puis diminue avec l'âge 🧬
miniature
Le Soleil bientôt en "zone de combat": une période de turbulences extrêmes ☀️
miniature
1
Les rhumatismes plus douloureux par temps humide: vrai ou faux ? 🌧️
miniature
Ce nouveau type de moteur repousse les limites du vol supersonique ✈️
miniature
Poster sur les réseaux sociaux peut nuire à votre santé mentale 🧠
miniature
Une super-Terre entre Mars et Jupiter ? 🌎
miniature
Découverte impressionnante d'un fossile de crocodile géant 🐊
miniature
1
Cet accident en laboratoire pourrait transformer drastiquement la mémoire numérique ⚡
miniature
1
Un virage technologique révèle l'impact du diabète gestationnel 🩺
miniature
Insolite: ces loups butinent des fleurs ! Des grands carnivores pollinisateurs ? 🌼
miniature
1
Ce fin gilet robotisé soulage les tâches répétitives 🦾
miniature
Les équations d'Einstein invalidées ? 👀
miniature
Ce tatouage électronique se connecte à votre cerveau 🧠
miniature
Cette IA de Google prédit la météo mieux que jamais, et sur 15 jours ! 🌦️
miniature
Des plats au bœuf... sans bœuf ? 🥩
miniature
2
Ce moteur de recherche d'un nouveau genre bouscule nos habitudes 🔍
miniature
Pourquoi les cheveux bouclent-ils en fonction de la météo ? 🌦️
miniature
Découverte: d'autres univers plus propices à la vie que le notre 👽
miniature
Ces sons urbains qui minent notre santé mentale 🚗
miniature
La testostérone impacte-t-elle vraiment le désir sexuel des hommes ? 🔥
miniature
Des microalgues éliminent les métaux lourds: voici comment 🧪
miniature
1
Et voici un qubit mécanique ! 🖥️
miniature
Les lentilles de contact sont-elles vraiment sans danger ? 👁️
miniature
Dans la course à l'IA générative, Google lance son générateur de vidéos 🎥
miniature
4
Une zone oubliée du cerveau permet aux paralysés de marcher à nouveau 🧠
miniature
Cette astuce quotidienne ajoute 11 ans à votre vie 🕒
miniature
Révolutions, migrations des européens... les éruptions volcaniques ont influencé l'histoire 🌋
miniature
Soit l'énergie noire n'est pas constante, soit une seconde force inconnue est à l'œuvre... 🌀
miniature
Voici pourquoi l'alcool peut rendre agressif 🥂
miniature
Expérience inédite: ce laser projette une ombre visible 💥
miniature
Ce plat millénaire réduit significativement la graisse corporelle 🍽️
miniature
Les scientifiques trompés ? La Voie Lactée n'est PAS comme les autres galaxies 🔭
miniature
Pourquoi ce que pensent les autres de nous nous fait tant ruminer ? 🧠
miniature
De la vie découverte sur un échantillon de l'astéroïde Ryugu (oups) 👽
Page générée en 0.297 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales | Partenaire: HD-Numérique
Version anglaise | Version allemande | Version espagnole | Version portugaise