Matrice transposée - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La matrice transposée (on dit aussi la transposée) d'une matrice
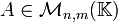
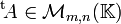
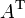
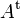
Si B = tA alors
![\forall {(i,j) \in [\![1;m]\!]\times[\![1;n]\!]},\qquad b_{i,j} = a_{j,i}\,](https://static.techno-science.net/illustration/Definitions/autres/f/fdef7552e9acd5bedc96e18b7f6bda2b_286ddac8d7c92a17d887471d7a47b732.png)
Exemple : si
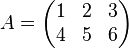
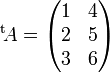
Propriétés
- L'application "transposition" est linéaire :
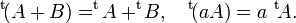
- La transposée de
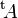
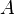
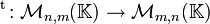
- La transposée du produit de deux matrices est égale au produit des transposées de ces deux matrices, mais dans l'ordre inverse :
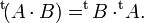
- Si une matrice est inversible (donc carrée) alors la transposée de son inverse est égale à l'inverse de sa transposée :
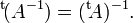
- Si
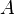
![\forall {i \in [\![1;n]\!]},\qquad b_{i,i} = a_{i,i}.](https://static.techno-science.net/illustration/Definitions/autres/f/fe7dda12c5d7d78558d84a04115513ea_e676e1f1a242860a900091d945cf8660.png)
- En particulier, toute matrice diagonale est symétrique, c'est-à-dire égale à sa transposée.
Interprétation : dualité
Dans le cadre des espaces euclidiens, si A représente une application linéaire f:E→F par rapport à deux bases orthonormales BE, BF alors sa transposée tA représente la matrice, dans les bases BF, BE , de son opérateur adjoint f*:F→E, caractérisé par :
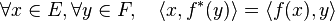
Plus généralement, si A représente une application linéaire par rapport à deux bases, alors sa transposée tA représente la matrice de la transposée de l'application par rapport aux bases duales (voir espace dual).

















































