Opérateur adjoint - Définition

Introduction

En mathématiques l'adjoint d'un opérateur, quand il existe, est un nouvel opérateur défini sur un espace vectoriel sur le corps des nombres réels ou complexes, muni d'un produit scalaire. Un tel espace est qualifié de préhilbertien.

Si l'opérateur initial est continu et si l'espace vectoriel est complet l'adjoint est toujours défini. Cette configuration se produit toujours en dimension finie. L'application qui, à un opérateur associe son adjoint, est semilinéaire continue bijective. Cette fonction est même une isométrie involutive. L'espace des opérateurs se décompose en deux sous-espaces vectoriels supplémentaires orthogonaux. Ce sont des espaces propres de l'application associés aux valeurs propres 1 et -1.

Certains opérateurs disposent d'une compatibilité vis-à-vis du produit scalaire. Tel est le cas si un opérateur commute avec son adjoint. Il est alors dit normal. Trois cas sont importants, les autoadjoints (resp. antisymétriques) correspondant à un opérateur adjoint de lui-même (resp. dont l'adjoint est son opposé) et orthogonaux dont l'adjoint est l'inverse. Sur un espace vectoriel complexe, le terme utilisé est unitaire et non plus orthogonal.

La notion d'adjoint d'un opérateur possède de nombreuses applications. En dimension finie et sur le corps des nombres complexes, la structure des endomorphismes normaux est simple, ils sont diagonalisables dans une base orthonormale. Le cas de la dimension infinie est plus complexe. Il est important en analyse fonctionnelle. Le cas autoadjoint est particulièrement étudié, il fournit le cadre le plus simple de la théorie spectrale. En algèbre générale, une algèbre stellaire correspond à une structure abstraite d'espace vectoriel munis d'une loi de composition interne analogue à la composition des opérateurs et d'une opération étoile ayant les mêmes propriétés que l'application qui, à un opérateur associe son adjoint.

Définitions

L'adjoint d'un opérateur est une notion correspondant à des situations fort différentes. Elle peut être appliquée dans le cas d'un espace euclidien ou hermitien, c'est-à-dire en dimension finie. Elle est aussi utilisée dans le contexte le plus simple de l'analyse fonctionnelle, c'est-à-dire dans un espace de Hilbert ou un préhilbertien. Elle peut enfin s'appliquer dans un cadre très général sur des espaces de Banach. Pour cette raison deux définitions se côtoient.

Préhilbertien

Cette définition couvre dans la pratique deux cadres théoriques un peu différents. Celui de la dimension finie et celui où aucune hypothèse n'est faite sur la dimension. Il correspond aussi à un premier cas d'analyse fonctionnelle, le plus simple. En général l'espace vectoriel choisi est un Hilbert, c'est-à-dire que la topologie associée à la distance est complète. Comme il est relativement facile de compléter un préhilbertien et que les théorèmes dont on disposent sont beaucoup plus nombreux, ce cadre est largement utilisé. Une unique définition permet de couvrir ces deux cas :

Soit H un espace préhilbertien sur un corps égal à celui des réels ou des complexes . Le produit scalaire est noté (.,.) dans cet article. Soit a et a^* deux opérateurs de E.

• Définition : L'opérateur a^* est dit adjoint de a si et seulement si la propriété suivante est vérifiée :

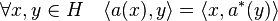
Il est d'usage de noter avec le signe * l'adjoint d'un opérateur. Le terme d'opérateur est en général celui utilisé pour désigner une application linéaire.

Algèbre stellaire

Comme la suite de l'article le montre l'application *, qui à un endomorphisme associe son adjoint est une application semilinéaire de l'espace des endomorphismes. Cet espace dispose, avec la composition des endomorphismes d'une structure d'algèbre. Une application *, disposant des mêmes caractéristiques que l'application adjointe et définie sur une algèbre est le cadre d'une structure appelée algèbre stellaire. L'image d'un élément a par l'application * est appelé adjoint de a.

Banach

En analyse fonctionnelle, tous les espaces ne disposent pas d'un produit scalaire. L'approche par les adjoints reste néanmoins fructueuse. L' opérateur a dispose de propriétés plus pauvres que celles du paragraphe précédent.

Dans le cas général, il n'est plus borné, c'est-à-dire qu'il n'existe pas nécessairement de majorant de la norme de l'image d'un vecteur de la boule unité. Ainsi la dérivée d'une fonction de la variable réelle dans l'ensemble réelle à support compact, infiniment différentiable et majorée en valeur absolue par un n'est pas majorée par une constante indépendante de la fonction. Cet espace muni de la norme de la convergence uniforme est important pour la définition des distributions. La dérivée est un opérateur linéaire non borné qui joue un grand rôle en analyse fonctionnelle.

Un opérateur a n'est pas nécessairement défini sur tout le Banach. Ainsi la fonction dérivée n'est pas définie sur toute fonction de ]-1/2, 1/2[ dans R et intégrable en valeur absolue. Pour la même raison que celle du paragraphe précédent, il est néanmoins utile de considérer cet opérateur.

Dans ce paragraphe, E et F désigne deux Banach, a un opérateur non borné de E dans F, E^* et F^* désignent les duaux topologiques de E et F. Dans la suite de l'article le terme dual signifie dual topologique. Il est en effet plus utilisé que le dual algébrique dans ce contexte. Le terme D(a) désigne le domaine de a, c'est-à-dire le sous-espace vectoriel sur lequel a est défini. Il est supposé dense dans E. La notation <.,.>_E (resp. <.,.>_F) désigne le crochet de dualité, il correspond à l'application bilinéaire de E^*xE (resp. F^*xF) qui à un couple formé d'une forme linéaire et d'un vecteur de E (resp. F) associe un scalaire.

• Définition : Le domaine noté D(a^*) de l'opérateur adjoint de a est le sous-ensemble de F^* suivant :

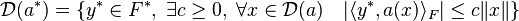
Cette définition permet la suivante :

• Définition : l'opérateur adjoint a^* de a est l'opérateur de D(a^*) dans E^* vérifiant l'égalité :

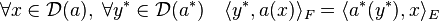
Il est fréquent que E et F soit confondu, l'adjoint est alors un opérateur de E^*.