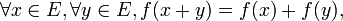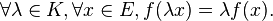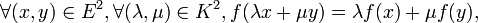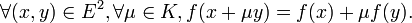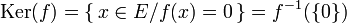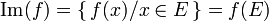Application linéaire - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, une application linéaire (aussi appelée opérateur linéaire ou transformation linéaire) est une application entre deux espaces vectoriels qui respecte l’addition des vecteurs et la multiplication scalaire définie dans ces espaces vectoriels, ou, en d’autre termes, qui « préserve les combinaisons linéaires ».
Définitions
Soit ƒ une application de E dans F où E et F sont deux espaces vectoriels sur un corps K.
L'application ƒ est une application linéaire (ou morphisme de K-espaces vectoriels) si et seulement si :
Une application ƒ possédant la première propriété est dite additive, et, pour la seconde, homogène. Elle possède ces deux propriétés à la fois si et seulement si :
ou plus simplement, si et seulement si :
- Un isomorphisme est un morphisme bijectif.
- Un endomorphisme est un morphisme ayant même espace vectoriel de départ et d'arrivée.
- Un automorphisme est un endomorphisme bijectif.
- Si l'espace vectoriel d'arrivée est le corps K on parle de forme linéaire.
On note
- LK(E,F) l’espace vectoriel des applications linéaires de E dans F ;
- IsomK(E,F) l’ensemble des isomorphismes de E dans F;
- LK(E) l’espace vectoriel des endomorphismes de E ;
- GLK(E) (appelé aussi le groupe linéaire) le groupe des automorphismes de E.
(Le corps K en indice est parfois omis et implicite.)
Exemples
- l'endomorphisme appelé homothétie vectorielle de rapport a :
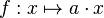
- l’application dérivation, de l'espace des applications dérivables de R dans R vers l'espace de toutes les applications de R dans R :
- d :
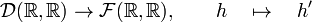
- d :
Noyau et Image
Si ƒ est une application linéaire de E dans F, le noyau de ƒ, noté Ker(ƒ), et l’image de ƒ, notée Im(ƒ), sont définis par
Ker provient de Kern, traduction de « noyau » en allemand. Im provient de image. L'ensemble Ker(ƒ) est un sous-espace vectoriel de E et l'ensemble Im(ƒ) est un sous-espace vectoriel de F. Plus généralement,
- L'image réciproque d'un sous-espace vectoriel de F par f est un sous-espace vectoriel de E ;
- Et l'image directe d'un sous-espace vectoriel de E par f est un sous-espace vectoriel de F.
Le théorème de factorisation affirme que f induit un isomorphisme de l'espace vectoriel quotient E/kerf sur l'image im f. Deux espaces isomorphes ayant même dimension, il suit la relation suivante, valable pour un espace E de dimension finie, appelée théorème du rang :
-
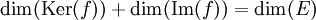
Le nombre dim( Im(ƒ) ) est aussi appelé rang de ƒ et est noté rg(ƒ).
Propriétés
-
- L'ensemble L(E,F) des applications linéaires de E dans F est un espace vectoriel.
En effet, L(E, F) est un sous-espace vectoriel de l'espace vectoriel des applications de E dans F. Il est non vide car contient l'application nulle. Si a et b sont deux applications linéaires, leur somme est toujours linéaire. On remarque enfin que si λ est un élément de K, l'application λa est aussi linéaire.
-
- La composée de deux applications linéaires est linéaire. Plus précisément :
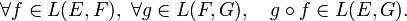
-
- Une application linéaire ƒ de L(E, F) est entièrement déterminée par l'image par ƒ d'une base de E.
En effet, soient (ei) (pour i élément de I) une base de E et x un vecteur de E. Alors il existe une unique famille presque nulle (λi) de coefficients telle que :

La linéarité de ƒ montre que l'image de x est parfaitement déterminée par la connaissance des images de la base :
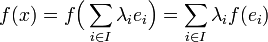
-
- Si E et F sont des espaces vectoriels de dimension finie alors la dimension de L(E,F) est finie aussi, et égale au produit de la dimension de E par la dimension de F.
Pour déterminer la dimension de L(E, F) le plus simple est de déterminer une base de cet espace. Soient (ei), pour i variant de 1 à n, une base de E et (fj), pour j variant de 1 à m, une base de F. Soit aαβ l'unique application linéaire telle que aαβ(eα)=fβ et pour tout i est différent de α, aαβ(ei)= le vecteur nul.
La famille d'applications linéaires (aij) est libre. En effet considérons une combinaison linéaire c non nulle de cette famille :
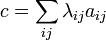
Au moins un coefficient λαβ est non nul. Alors c(eα) est non nul car son coefficient sur pour le vecteur fβ est non nul, ce qui montre que c est non nulle. La seule combinaison linéaire nulle est triviale, ce qui montre que la famille est libre.
La famille (aij) est génératrice. Soit b un élément de L(E, F). Notons μij les coordonnées du vecteur ei dans la base considérée de F. Soit b' l'application linéaire définie par :
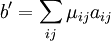
Les applications b et b' sont confondues sur une base de l'ensemble de départ. Elles sont toutes deux linéaires et donc égales. Ainsi, toute application linéaire de L(E, F) est combinaison linéaire de la famille, ce qui démontre son caractère générateur.
Le cardinal de cette base est bien le produit de la dimension de E par celle de F, ce qui termine la démonstration.
-
- Le calcul de l'image d'un vecteur par une application linéaire à l'aide de l'utilisation d'une base utilise le concept de matrice.