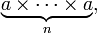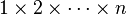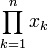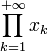Multiplication - Définition

Multiplications de plusieurs termes entre eux

Puisque la multiplication est associative, il est inutile de définir une priorité sur les multiplications à effectuer. Il reste cependant à définir comment écrire le produit d'un nombre indéterminé de termes.

signifie que l'on a multiplié n fois le terme "a" par lui-même. le résultat est noté aⁿ et se lit "a à la puissance n"

signifie que l'on a fait le produit de tous les entiers de 1 à n, le résultat est noté n! et se lit "factorielle n"

Si (x_i) est une suite de nombres, signifie que l'on a fait le produit de ces n facteurs entre eux. Ce produit est aussi noté

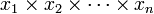
Si l'expression a un sens, la limite du produit précédent quand n tend vers l'infini est appelé produit infini et se note