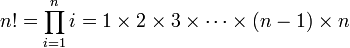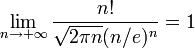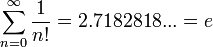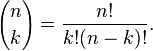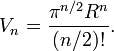Factorielle - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, la factorielle d'un entier naturel n, notée n!, ce qui se lit soit « factorielle de n » soit « factorielle n », est le produit des nombres entiers strictement positifs inférieurs ou égaux à n. La notation n! a été introduite en 1808 par Christian Kramp.
La factorielle joue un rôle important en algèbre combinatoire parce qu'il y a n! façons différentes de permuter n objets. Elle apparaît dans de nombreuses formules en mathématiques, comme par exemple la formule du binôme et la formule de Taylor.
Définition
| n | n! |
|---|---|
| 0 | 1 |
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 24 |
| 5 | 120 |
| 6 | 720 |
| 7 | 5 040 |
| 8 | 40 320 |
| 9 | 362 880 |
| 10 | 3 628 800 |
| 11 | 39 916 800 |
| 12 | 479 001 600 |
| 13 | 6 227 020 800 |
Soit n un entier naturel. Sa factorielle est formellement définie par :
Le tableau de droite donne les premières factorielles ; par exemple, on a
- 1! = 1
- 2! = 1 × 2 = 2
- 3! = 1 × 2 × 3 = 6
- 4! = 1 × 2 × 3 × 4 = 24
- 10! = 1 × 2 × 3 × 4 × 5 × 6 × 7 × 8 × 9 × 10 = 3 628 800
Par convention :
- 0! = 1
La définition de la factorielle sous forme de produit rend naturelle cette convention puisque 0! est un produit vide, c'est-à-dire réduit à l'élément neutre de la multiplication. Cette convention est pratique pour plusieurs autres raisons :
- Elle permet une définition récursive de la factorielle : (n+1)! = n! × (n+1) pour tout n.
- Elle permet à des formules de dénombrement obtenues en analyse combinatoire d'être encore valides pour des tailles nulles. En particulier, le nombre d'arrangements ou de permutations de l'ensemble vide est égal à 1.
- La fonction Gamma (définie plus bas) permet alors d'écrire Γ(n + 1) = n! pour tout n.
La formule de Stirling donne un équivalent de n! quand n est grand :
d'où
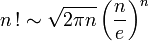
La somme des inverses des factorielles donne un nombre très connu des mathématiciens, la constante e.
Exemples d'applications
- En combinatoire, il existe n! façons différentes d'arranger n objets distincts (c’est-à-dire n! permutations). Et le nombre de façons de choisir k éléments parmi un ensemble de n est donné par le coefficient binomial :
- En permutation, si r éléments peuvent être choisis et arrangés de r façons différentes parmi un total de n objets (r < n), alors le nombre total de permutations distinctes est donné par :
- nPr =
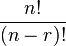
- Les factorielles apparaissent également en analyse. Par exemple, le théorème de Taylor, qui exprime la valeur en x d'une fonction f sous forme de série entière, fait intervenir la factorielle n! pour le terme correspondant à la ne dérivée de f en x.
- Le volume d'une hypersphère en n dimensions peut être exprimé par :
- Les factorielles sont utilisées de façon intensive en théorie des probabilités.
- Les factorielles sont souvent utilisées comme exemple — avec la suite de Fibonacci — pour l'apprentissage de la récursivité en informatique du fait de leur définition récurrente simple.