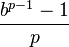Nombre cyclique - Définition

Introduction

Un nombre cyclique, ou nombre phénix, est un entier dont les permutations circulaires des chiffres correspondent aux multiples du nombre. Le plus connu est 142857:

142857 × 1 = 142857

142857 × 2 = 285714

142857 × 3 = 428571

142857 × 4 = 571428

142857 × 5 = 714285

142857 × 6 = 857142

Cas spéciaux

Si les zéros ne sont pas permis au début des nombres, alors 142857 est le seul nombre cyclique décimal. Par contre, s'ils sont permis, la séquence des nombres cycliques commence comme suit :

142857 (6 chiffres)

0588235294117647 (16 chiffres)

052631578947368421 (18 chiffres)

0434782608695652173913 (22 chiffres)

0344827586206896551724137931 (28 chiffres)

0212765957446808510638297872340425531914893617 (46 chiffres)

0169491525423728813559322033898305084745762711864406779661 (58 chiffres)

016393442622950819672131147540983606557377049180327868852459 (60 chiffres)

Pour être cyclique, seuls les multiples successifs du nombre doivent être considérés et ceux-ci doivent correspondre à des permutations circulaires du nombre. Ainsi, le nombre 076923 n'est pas considéré comme cyclique, même si toutes ses permutations circulaires sont des multiples, car ceux-ci ne sont pas successifs :

076923 × 1 = 076923

076923 × 3 = 230769

076923 × 4 = 307692

076923 × 9 = 692307

076923 × 10 = 769230

076923 × 12 = 923076

Cette restriction exclut aussi des cas triviaux tels :

1. chiffres répétés, par exemple : 555
2. nombres cycliques répétés, par exemple : 142857142857
3. chiffres uniques précédés de zéros, par exemple : "005"

Les chiffres uniques peuvent être considérés comme des nombres cycliques triviaux ou dégénérés.

Formes de nombres cycliques

En s'appuyant sur leur relation aux fractions unitaires, on démontre que les nombres cycliques sont de la forme

où b est la base (10 dans le cas du système décimal) et p est un nombre premier ne divisant pas b. Les nombres premiers p qui génèrent des nombre cycliques sont appelés nombres premiers longs.

Par exemple, le cas b = 10, p = 7 donne le nombre cyclique 142857.

Toutes les valeurs de p ne généreront pas forcément un nombre cyclique selon cette formule; par exemple p = 13 donne 076923076923. Ces cas erronés contiendront toujours une ou plusieurs répétition de chiffres.

Les premières valeurs de p pour lesquels cette formule produit un nombre cyclique en notation décimale sont (séquence A001913 dans l'OEIS) :

7, 17, 19, 23, 29, 47, 59, 61, 97, 109, 113, 131, 149, 167, 179, 181, 193, 223, 229, 233, 257, 263, 269, 313, 337, 367, 379, 383, 389, 419, 433, 461, 487, 491, 499, 503, 509, 541, 571, 577, 593, 619, 647, 659, 701, 709, 727, 743, 811, 821, 823, 857, 863, 887, 937, 941, 953, 971, 977, 983 …

Le patron de cette séquence est issu de la théorie algébrique des nombres. Plus spécifiquement, cette séquence est définie comme l'ensemble des nombres premiers p tels que 10 est une racine primitive modulo p. Une conjecture d'Emil Artin [1] postule que cette séquence contiendrait 37.395..% des nombres premiers.

Relation avec les décimales récurrentes

Les nombres cycliques sont liés aux décimales récurrentes des fractions unitaires. En général, pour un nombre cyclique de longueur L, le développement décimal de

1/(L + 1)

a une période de L, et répète le nombre cyclique.

Par exemple :

1/7 = 0.142857142857…

Les multiples de ces fractions présentent des permutations circulaires :

1/7 = 0.142857142857…

2/7 = 0.285714285714…

3/7 = 0.428571428571…

4/7 = 0.571428571428…

5/7 = 0.714285714285…

6/7 = 0.857142857142…

En contrepartie, si la période du développement décimal de 1/p est

p − 1,

alors les chiffres répètent un nombre cyclique.