Développement décimal - Définition

Introduction

En mathématiques, le développement décimal est une façon d'écrire des nombres réels positifs à l'aide des puissances de 10 (négatives ou positives). Lorsque les nombres sont des entiers naturels, le développement décimal correspond à l'écriture en base 10. Lorsqu'ils sont décimaux, on obtient un développement décimal limité. Lorsqu'ils sont rationnels, on peut obtenir un développement décimal illimité périodique. Enfin, lorsqu'ils sont irrationnels, le développement décimal est illimité et non périodique.

Cas des nombres entiers

Tout nombre entier possède une écriture décimale qui nous est naturelle car enseignée depuis notre enfance. Nous prenons conscience du fait qu'il ne s'agit que d'une écriture lorsque les circonstances nous mettent en contact avec d'autres systèmes de numération.

Exemple : 123 827 = 1×10⁵ + 2×10⁴ + 3×10³ + 8×10² + 2×10¹ + 7×10⁰

Cas des nombres rationnels

Aborder l'écriture décimale de certains nombres rationnels nous fait rentrer dans le monde de l'infini car l'écriture ne s'arrête jamais. On parle de développement décimal illimité.

exemple: Division de 13 par 7

      13          |7       60         |1,85714285...        40        |         50       |          10      |           30     |            20    |             60   |              40  |      

Puisque l'on obtient de nouveau le reste 6 (avant dernière ligne), en abaissant le 0, on se trouvera à diviser encore 60 par 7 à réobtenir pour quotient 8, pour reste 4 etc. Le cycle 857142 s'appelle la période du développement décimal illimité périodique. On écrira .

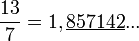
La période du développement décimal ne commence pas toujours juste après la virgule : .

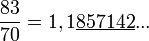
On peut démontrer que tout nombre rationnel possède un développement décimal illimité périodique. Pour le comprendre, il suffit de généraliser le principe de la division précédente. Supposons que l'on divise P par Q, dans la division de P par Q, on est amené, pour les décimales après la virgule, à « abaisser des zéros ». Si le reste précédent est r, on cherche alors à diviser 10r par Q. Les restes de la division sont en nombre fini (0, 1, ..., Q - 1), donc on ne peut pas prolonger indéfiniment la division sans rencontrer deux restes identiques. Si on appelle r₁ et r'₁ les deux premiers restes identiques, on voit que la division de 10r₁ par Q sera identique à celle de 10r'₁ par Q, et donnera le même quotient q₁ = q'₁ et même reste r₂ = r'₂ et ainsi de suite.

Un nombre décimal possède aussi un développement décimal illimité de période 0.

Réciproquement, tout développement décimal illimité périodique correspond à l'écriture d'un rationnel.

Exemple : 3,25723723723... = x

100x = 325,723723723...

100x - 325 = y = 0,723723723... On peut remarquer que, si y est rationnel, x le sera aussi.

y = 0,723723....

1000y = 723,723723723...

1000y = 723 + y

999y = 723

. y est alors un rationnel et x aussi.

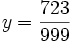
La méthode se généralise pour tout développement décimal illimité périodique. On se débarrasse de la mantisse par une multiplication par la puissance de 10 adéquate et par la soustraction d'un nombre entier. On obtient alors un nombre y s'écrivant 0,périodepériodepériode.... sur lequel on effectue le même type d'opération que plus haut : multiplication par la puissance de 10 adéquate 10ⁿy = période + y . La résolution de l'équation précédente prouve que y est rationnel et donc que x est rationnel.

Cette méthode de décalage sera employée par la suite pour calculer de façon analogue la somme des termes d'une suite géométrique.

Cas particulier de 0,99999999... = y.

En utilisant la technique précédente, on obtient 10y = 9,99999... = 9 + y. La résolution de l'équation précédente mène donc à y = 1.

1 possède donc deux « développements décimaux illimités » périodiques : 1,000000... et 0,9999.... Selon la définition d'un développement décimal illimité sur , seul sera retenu le premier développement illimité, le second s'appelant un développement impropre.