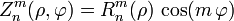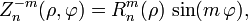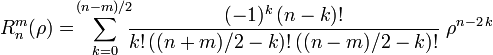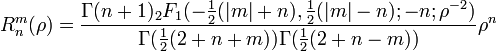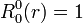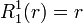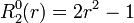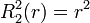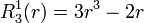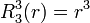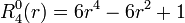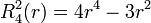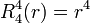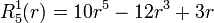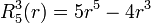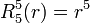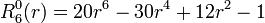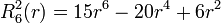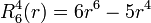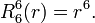Mercredi 10 Septembre 2025
Rechercher 🔍

Polynômes de Zernike - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - Définition des polynômes - Exemples

Introduction

Tracés des polynômes de Zernike sur le disque unité.

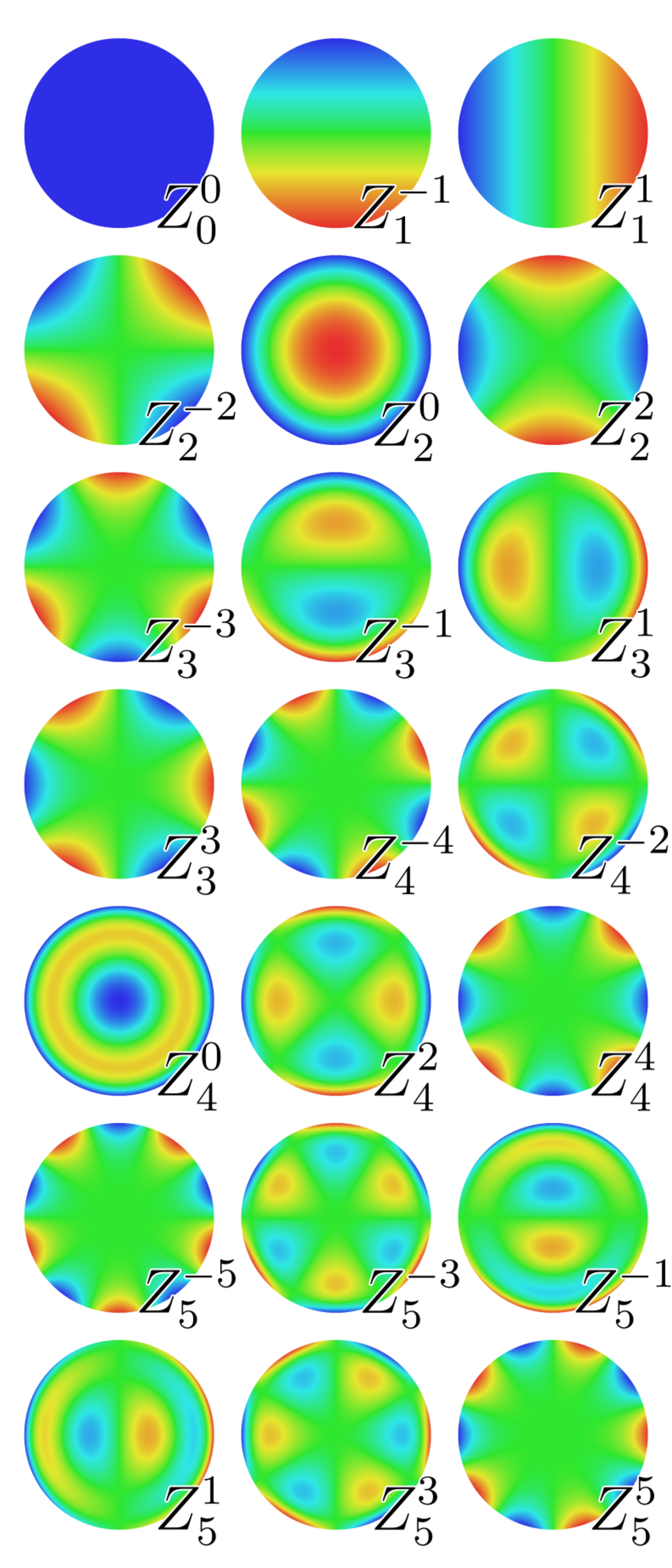
Les polynômes de Zernike sont une série de polynômes qui sont orthogonaux sur le disque unité. Ils portent le nom de Frits Zernike ; ils jouent un rôle important en optique géométrique.

Définition des polynômes

Les polynômes de Zernike peuvent se décomposer en fonctions paire et impaire. Les fonctions paires sont :

Z^{m}_n(\rho,\varphi) = R^m_n(\rho)\,\cos(m\,\varphi) \!

et les fonctions impaires sont :

Z^{-m}_n(\rho,\varphi) = R^m_n(\rho)\,\sin(m\,\varphi), \!

où m et n sont des nombres entiers naturels non nuls, avec n≥m, φ est l'angle d'azimuth exprimé en radians, et ρ est la distance radiale normalisée. Les polynômes radiaux Rmn sont définis tels que :

R^m_n(\rho) = \! \sum_{k=0}^{(n-m)/2} \!\!\! \frac{(-1)^k\,(n-k)!}{k!\,((n+m)/2-k)!\,((n-m)/2-k)!} \;\rho^{n-2\,k}

ou

R^m_n(\rho) = \frac{\Gamma(n+1){}_2F_{1}(-\frac{1}{2}(|m|+n),\frac{1}{2}(|m|-n);-n;\rho^{-2})}{\Gamma(\frac{1}{2}(2+n+m))\Gamma(\frac{1}{2}(2+n-m))}\rho^n

pour n − m pair, et sont égaux à 0 pour n − m impair.

Pour m = 0, le polynôme se réduit à Rn0(ρ).

Exemples

Les premiers polynômes de Zernike sont :

R^0_0(r) = 1 \,
R^1_1(r) = r \,
R^0_2(r) = 2r^2 - 1 \,
R^2_2(r) = r^2 \,
R^1_3(r) = 3r^3 - 2r \,
R^3_3(r) = r^3 \,
R^0_4(r) = 6r^4 - 6r^2 + 1 \,
R^2_4(r) = 4r^4 - 3r^2 \,
R^4_4(r) = r^4 \,
R^1_5(r) = 10r^5 - 12r^3 + 3r \,
R^3_5(r) = 5r^5 - 4r^3 \,
R^5_5(r) = r^5 \,
R^0_6(r) = 20r^6 - 30r^4 + 12r^2 - 1 \,
R^2_6(r) = 15r^6 - 20r^4 + 6r^2 \,
R^4_6(r) = 6r^6 - 5r^4 \,
R^6_6(r) = r^6. \,
- Introduction - Définition des polynômes - Exemples
miniature
💥 Et si un Univers avait existé avant le Big Bang... la réponse dans les simulations ?
miniature
🦋 Comment des papillons australiens parcourent jusqu'à 1000 km au printemps
miniature
📶 Ce système utilise les ondes Wi-Fi pour nous identifier
miniature
🌍 L'ozone pourrait réchauffer la Terre plus que prévu – Une surprise climatique
miniature
⚛️ Un "monde miroir" pour expliquer le mystère de la matière noire
miniature
💊 Découverte: ces médicaments courants réduisent aussi le risque de suicide, d'addictions et de délits
miniature
👽 Comment les médias parlent-ils de la vie extraterrestre ? Une étude scientifique dévoile tout !
miniature
🧠 Cette française a une capacité hors du commun: elle voyage mentalement dans le temps !
miniature
💀 Votre risque de mourir d'un astéroïde vs un accident de voiture: les chiffres étonnants
miniature
🦕 Ce squelette avait été oublié dans un musée, il s'agit en fait d'une espèce inconnue !
miniature
🧱 Malgré des atomes majoritairement vides, pourquoi ne peut-on pas traverser les murs ?
miniature
🍖 Ils mangeaient leurs voisins, sans nécessité
miniature
🌡️ La Méditerranée se tropicalise à vue d'œil
miniature
🧪 Cette étude révèle la liste des additifs alimentaires les plus dangereux pour votre santé
miniature
👀 Pas seulement Supermassif, mais Ultramassif ! Voici le plus imposant trou noir de l'Univers connu !
miniature
☕ Pourquoi votre café du matin a plus d'effet qu'à un autre moment de la journée ?
miniature
🍽️ Surprise: les épaississants alimentaires sont finalement digérés
miniature
⚛️ Voici ce qui rend la matière stable, visualisé pour la première fois
miniature
⚠️ Voici les réels dangers des produits ultra-transformés, et ce n'est pas dû aux calories !
miniature
🔭 Ces planètes de vapeur chamboulent nos modèles planétaires
miniature
🧠 Le risque réel de la pollution sur notre cerveau
miniature
🪐 Pourquoi les planètes ont-elles une orbite inclinée ? Un début de réponse !
miniature
1
⚡1000 Gb par seconde: une puce pour une IA ultra rapide
miniature
🌍 Un concours photo dévoile cette image choc d'un paresseux survivant dans un monde sans arbre
miniature
🌀 Cette galaxie montre que la vie a pu émerger rapidement après le Big Bang
miniature
🦴 Ces pattes de trilobites révèlent un dynamisme inattendu
miniature
🕰️ Ces vagues de sable sur Mars se déplacent à un rythme inimaginable
miniature
💀 Le mystère du crâne de Petralona impossible à dater
miniature
💥 Une collision entre deux planètes aurait engendré la vie
miniature
🍷 Un même circuit cérébral pour l'alcool et la nicotine
miniature
🔭 3I/ATLAS: le visiteur interstellaire avait déjà été enregistré dans le passé
miniature
1
🕵️‍♂️ Une étude révèle l'essor alarmant de la fraude scientifique organisée
miniature
💥 Ces ondes venues du Big Bang pourraient tout changer
miniature
🌍 Vers un basculement brutal de l'Amoc: les dernières prévisions sont alarmantes
miniature
💀 Découverte glaçante de sacrifices humains au Pérou il y a 2300 ans
miniature
🌔 Oxydation nocturne: un chaînon manquant des modèles climatiques
miniature
🦖 Certains dinosaures carnivores préféraient déchirer leurs proies plutôt que de les broyer
miniature
⚡ Cette fibre optique creuse promet de rendre Internet plus rapide et plus efficace
miniature
⛈️ Cette nouvelle catégorisation des ouragans reflète mieux leur dangerosité
miniature
📖 La lecture pour le plaisir est en fort déclin: les causes et les conséquences
miniature
2
🪐 Des trous noirs dévorant les planètes de l'intérieur
miniature
⌛ Vieillir en bonne santé: le secret pourrait se trouver dans notre peau
miniature
🏔️ L'Himalaya devrait s'effondrer sous son propre poids, à moins que...
miniature
⚡ Cette IA rend le transfert d'énergie sans fil plus stable et efficace que jamais
miniature
🌡️ Les vagues de chaleur nous feraient vieillir autant que le tabac ou l'alcool
miniature
👽 Une vie extraterrestre sur Cérès ?
miniature
🧠 Parkinson: le côté atteint prédit l'évolution de la maladie
miniature
🔭 Les aurores sur Jupiter présentent un comportement jusqu'alors inconnu
miniature
🍖 Découverte d'un prédateur hypercarnivore mangeur de dinosaures
miniature
🌟 Quelle est la plus grande étoile de l'Univers ?
Page générée en 0.287 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise