Racine d'un nombre complexe - Définition

Détermination continue

Si U est un ouvert de C, une détermination continue d'une racine carrée sur U est une application continue telle que f(z)² = z.

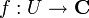
Il n'existe aucune détermination continue d'une racine carrée sur C-0.

Preuve.

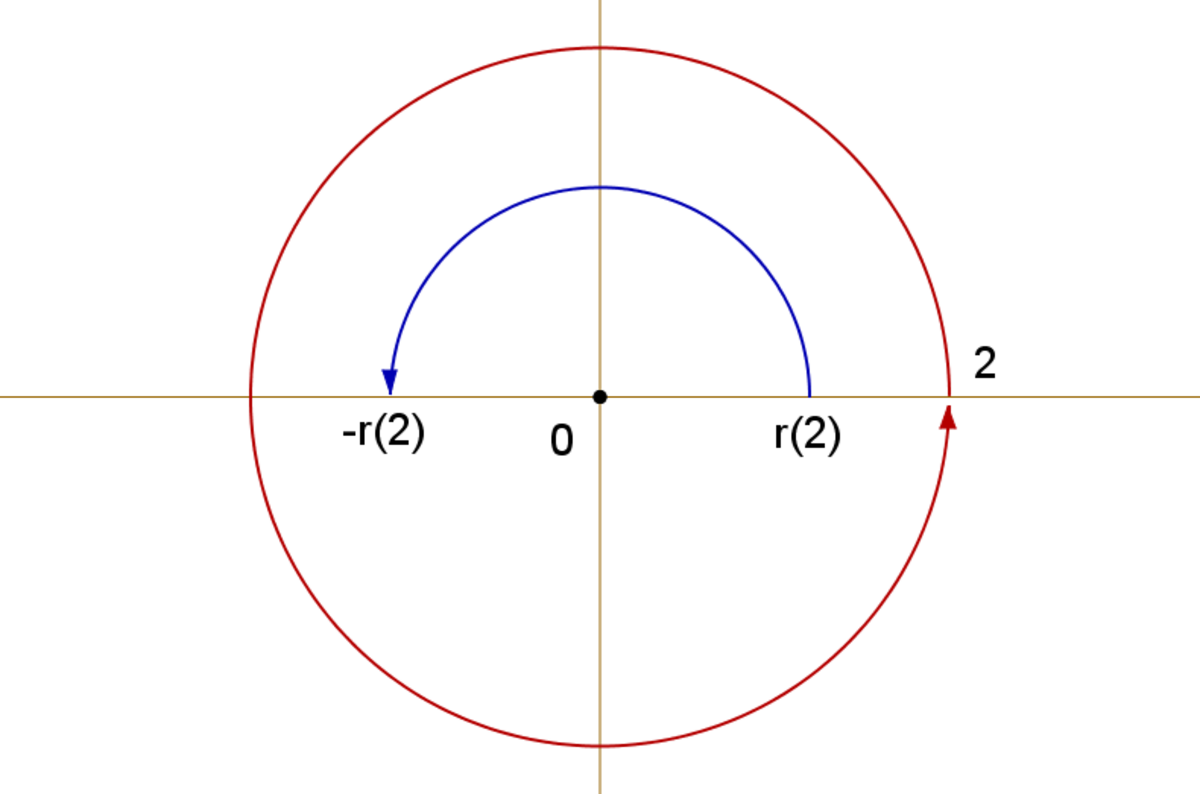
Sinon, on aurait une fonction continue qui à un nombre complexe z = re^iθ associe l'une de ses racines distinctes, ou bien , ou bien . La continuité de f implique que le signe reste constant lorsque r varie à θ fixé. Par conséquent, , où . Mais comme f doit être continue, ε doit être localement constant, et par conséquent, constant par un argument de connexité.

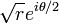
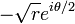
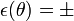
Par suite, . Mais alors, remplacer θ par θ + 2π pose problème. Le terme de droite devient alors que le terme de gauche reste inchangé. D'où une contradiction.

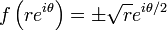
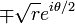
L'image à droite illustre la preuve. Pour un tour complet effectué le long d'un cercle de centre 0 implique de faire, le suivi continu d'une racine carrée ne parcours qu'un simple demi-tour.