Racine d'un nombre complexe - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Une racine carrée d'un nombre complexe z est un nombre complexe w vérifiant w2=z. Tout nombre complexe a exactement deux racines carrées distinctes, excepté 0, dont 0 est la seule racine carrée. Par exemple, les deux racines carrées de -1 sont i et -i où i est l'unité imaginaire. Plus généralement, une racine n-ième de z est un nombre complexe w vérifiant wn=z. Hormis 0, tout nombre complexe admet exactement n racines n-ièmes distinctes. Par exemple,
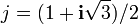
Les racines n-ièmes de l'unité 1 forment un groupe pour le produit, noté Un, qui est un groupe cyclique d'ordre n.
Il n'existe aucune détermination continue d'une racine carrée sur C. Plus exactement, il n'existe aucune application continue
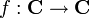
Formules
- Racines carrées en coordonnées cartésiennes.
- Racines k-ièmes en coordonnées polaires.
En coordonnées polaires, un nombre complexe s'écrit z = reiθ où r est positif. Si z est non nul, r est positif. Les racines k-ièmes de z sont les nombres complexes w tels que wk=z. Elles sont au nombre de k et sont explicitement données par :
-
![w=\sqrt[k]{r}e^{i\theta/k}e^{2i\pi q/k}](https://static.techno-science.net/illustration/Definitions/autres/9/99d56effbaf590c222a188dd18d71303_ed0860f5a2ce22c098bc0a8369d96b4a.png)
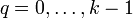
Pour k=2, on retrouve une description des racines carrées. La vérification est une application de la formule de Moivre.
Racines de l'unité
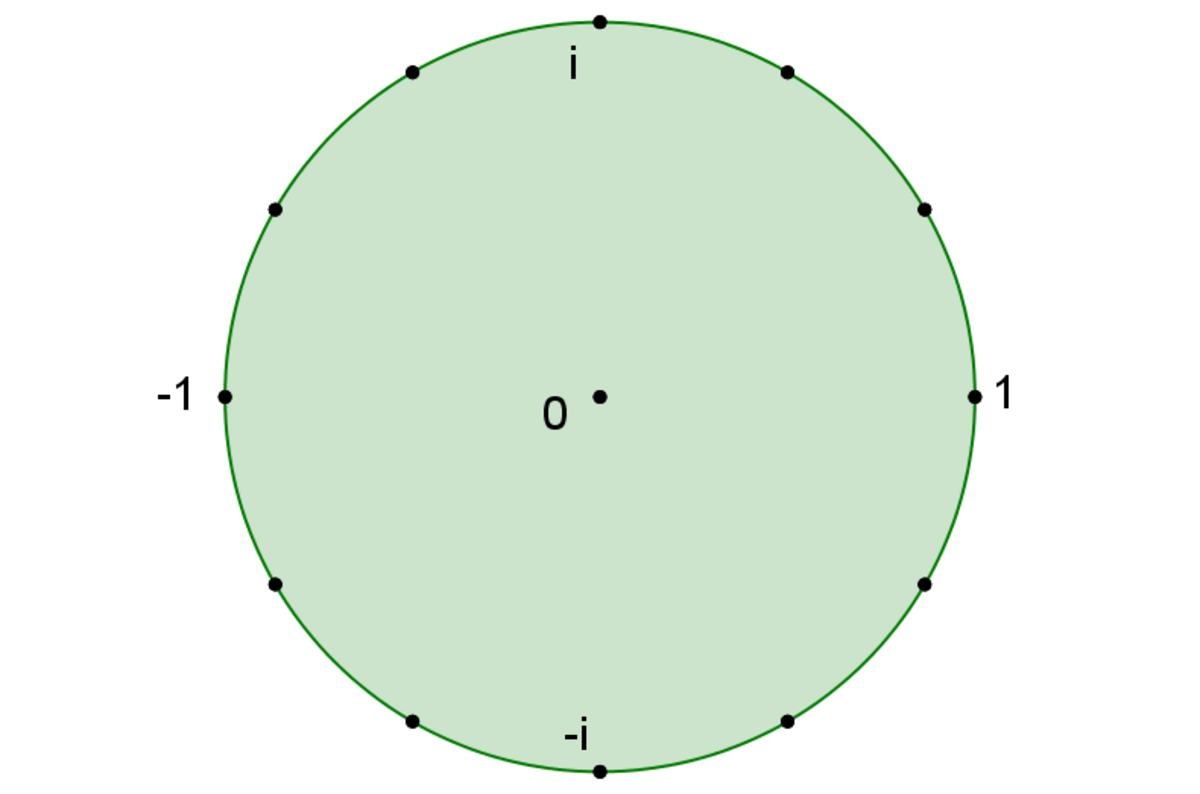
Les racines k-ièmes de l'unité 1 sont parfois appelées les nombres de Moivre. Le produit d'une racine n-ième de 1 et d'une racine k-ième de 1 est une racine r-ième de 1, où r = pgcd(k,n). En particulier, l'ensemble Uk des racines k-ièmes de 1 est stable par multiplication complexe. C'est un groupe fini. Les racines k-ièmes de 1 s'écrivent :
-
![\exp\left[2i\pi\frac{q}{k}\right]](https://static.techno-science.net/illustration/Definitions/autres/2/24a834420593a3c58bdd352082b5db62_fa7273365d1c7b7b32068b2d1cbbbfe7.png)
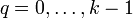
Le groupe Uk est cyclique et ses générateurs sont appelés les racines primitives de 1.
Toutes les racines k-ième de l'unité sont situées sur le cercle unité et sont les sommets d'un polygone régulier à k côtés ayant un sommet d'affixe 1.
Existence
Les formules ci-dessus démontrent l'existence des racines carrées et des racines k-ièmes de l'unité. Néanmoins, les formules pour les racines k-ièmes s'appuient sur la définition de l'exponentielle complexe et sur la formule de Moivre. Cette application se définit comme d'une série entière et est un exemple de fonction entière. Il est implicitement fait appel ici à l'analyse complexe.
Le théorème fondamental de l'algèbre

Le théorème fondamental de l'algèbre peut s'appliquer ici, et montre que tout nombre complexe non nul admet exactement k racines complexes distinctes.
Le théorème fondamental de l'algèbre possède de nombreuses preuves. Certaines sont détaillées dans l'article dédié. La plupart utilisent des outils de topologie et d'analyse, voire d'analyse complexe. L'appliquer ici pour éviter la formule de Moivre a un sens seulement si on dispose d'une preuve qui utilise l'algèbre seule. Une telle démonstration a été publiée par le collectif Nicolas Bourbaki en 1952, corrigeant une idée présentée par Laplace en 1795.
Utiliser la preuve attribuée à d'Alembert et à Argand ne serait pas valable ici. Cette preuve, en réalité achevée en 1941 par Littlewood, s'appuie sur une construction des racines k-ièmes des nombres complexes. Cette construction ne doit pas faire appel à la formule de Moivre.
Lemme de Littlewood
La démonstration du théorème fondamental de l'algèbre proposée par Littlewood en 1941[réf. souhaitée] est essentiellement celle donnée par d'Alembert et corrigée par Argand et Cauchy, à ceci près que dans le lemme d'existence d'au moins une racine k-ième pour chaque nombre complexe, on évite d'utiliser la formule de Moivre : on s'appuie sur la définition des racines sur R+ et on fait appel à un peu de topologie.
- On démontre d'abord que si k est impair, tout complexe z non nul a au moins une racine k-ième. La méthode (analogue à celle de Cauchy pour la preuve du théorème fondamental) est de poser Q(X) = Xk − z, de choisir un complexe w réalisant le minimum de | Q(w) | sur le plan complexe, et de montrer que Q(w) = 0.
- On commence par montrer que w est non nul. Pour cela, on pose u0 = z / | z | (qui est un nombre complexe de module 1), on choisit u parmi 1, -1, i et -i de telle sorte que | u − u0 | < 1, et l'on pose v=uk. Ainsi
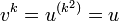
![y=\sqrt[k]{|z|}v](https://static.techno-science.net/illustration/Definitions/autres/4/4ecd9145c2afea810a938474dbd19dff_58ce9ee4505bf5431013cbfe1966b435.png)
- On en déduit ensuite que Q(w) = 0. Pour cela, on écrit Q(w + h) = (wk − z) + kwk − 1h + h2R(h) pour un certain polynôme R. Pour
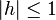
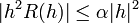
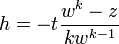
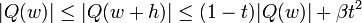 , si bien que
, si bien que
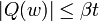
- On commence par montrer que w est non nul. Pour cela, on pose u0 = z / | z | (qui est un nombre complexe de module 1), on choisit u parmi 1, -1, i et -i de telle sorte que | u − u0 | < 1, et l'on pose v=uk. Ainsi
- On étend ensuite le résultat précédent à tout entier k>0, par récurrence sur sa 2-valuation, c'est-à-dire sur le plus grand entier r tel que k soit divisible par 2r.
- Le cas r=0 correspond au cas k impair déjà vu.
- L'étape de récurrence se fait en remarquant que si k=2q et si w est l'une des deux racines carrées de z (fournies par des formules en coordonnées cartésiennes), toute racine q-ième de w est racine k-ième de z.
Une fois établi ce lemme (d'existence d'au moins une racine k-ième), la démonstration du théorème fondamental de l'algèbre se poursuit de manière identique à celle donnée par d'Alembert et corrigée par Argand et Cauchy. On déduit alors de ce théorème (cf supra) que tout nombre complexe non nul admet exactement k racines k-ièmes complexes.

















































