Système duodécimal - Définition

Fractions

Certaines fractions s'expriment de manière très simple dans le système duodécimal, comme par exemple :

1 / 2 = 0,6

1 / 3 = 0,4

1 / 4 = 0,3

1 / 6 = 0,2

1 / 8 = 0,16

1 / 9 = 0,14

D'autres s'expriment de manière plus compliquée (X = dix, E = onze) :

1 / 5 = 0,2497 2497 avec chiffres périodiques (nombre que l'on peut arrondir à 0,25)

1 / 7 = 0,186X35 186X35 avec chiffres périodiques

1 / X = 0,1 2497 2497 avec chiffres périodiques (nombre que l'on peut arrondir à 0,125)

Quelle que soit la base utilisée, une fraction peut s'exprimer en numération de position avec un nombre fini de chiffres si et seulement si tous les facteurs premiers du dénominateur sont des diviseurs de cette base.

Ainsi, en base 10 (= 2 × 5), les fractions dont les dénominateurs sont constitués de multiples de 2 ou 5 sont finies :

,

,

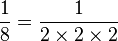
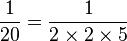
et

=

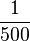
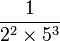
peuvent être exprimées exactement avec un nombre fini de chiffres après la virgule comme 0,125, 0,05, et 0,005 respectivement. Cependant,

et

donnent les répétitions 0,333... et 0,142857 142857...

Dans le système duodécimal (= 2×2×3) :

1 / 8 s'exprime exactement avec un nombre fini de chiffres après la virgule ;

1 / 20 et 1 / 500 nécessitent une répétition périodique de chiffres après la virgule parce que leurs dénominateurs incluent 5 dans leur décomposition ;

1 / 3 s'exprime exactement avec un nombre fini de chiffres après la virgule ;

1 / 7 nécessite une répétition périodique de chiffres après la virgule, comme en base 10.

On peut argumenter que les facteurs de 3 sont plus facilement rencontrés dans la vraie vie que ceux de 5 lors des divisions. Mais en pratique, la gêne occasionnée par la périodicité des fractions est moins courante lorsque le système duodécimal est utilisé. Cela est particulièrement vrai dans les calculs financiers, lorsque les 12 mois de l'année entrent en ligne de compte dans les calculs.