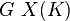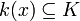Variété algébrique - Définition
La liste des auteurs de cet article est disponible ici.
Bibliographie
A. Grothendieck, J. Dieudonné: Éléments de géométrie algébrique, édition 1971, Chapitre I, appendice.
Points à valeurs dans une extension
Soit X une variété algébrique sur un corps k. On fixe une clôture algébrique
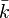
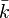
En effet, localement X est une variété affine égale à
![\mathrm{Spm }(k[T_1, \ldots, T_n]/I)](https://static.techno-science.net/illustration/Definitions/autres/5/5133063e0f681d169c54c7df6bd9b0af_a2edcd4f22c065f498d4641ba141f357.png)
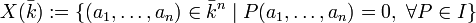
possède une application canonique
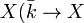
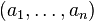
![( (T_1-a_1, \ldots, T_n-a_n)\bar{k}[T_1, \ldots, T_n]\cap k[T_1,\ldots, T_n])/I.](https://static.techno-science.net/illustration/Definitions/autres/0/052fcb8c76db6b9bff3674bd33564541_64a5dbdee42086d717df617ac6ea0063.png)
Cette application est surjective, de sorte que tout point de X peut être vu comme un point (non unique) de
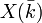
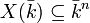
Si K est une sous-extension de
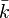
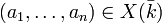
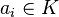
Si K / k est galoisienne de groupe de Galois G, alors G opère sur X(K) coordonnée par coordonnée. L'ensemble des orbites