Variété algébrique - Définition
La liste des auteurs de cet article est disponible ici.
Points rationnels
Le théorème des zéros de Hilbert décrit une bijection entre les points de l'espace affine
![\mathrm{Spm} k[T_1, \ldots, T_n]](https://static.techno-science.net/illustration/Definitions/autres/b/bed793fa82982acf98d36fe490759a48_3d0a061944fe20eb6fbfe4ebde11e3e2.png)
Soit X une variété algébrique sur un corps k. Un point x de X est appelé un point rationnel (sur k) si le corps résiduel OX,x / mx en x, qui contient toujours k, est égal à k. L'ensemble des points rationnels de X est noté X(k). Un point d'une sous-variété est rationnel si et seulement s'il est rationnel vu comme point dans la variété ambiante.
Si
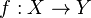
Un point d'une variété algébrique affine associée à
![A=k[T_1,\ldots, T_n]/I](https://static.techno-science.net/illustration/Definitions/autres/6/6ef4ccbfacce9925b3c31f59d47b4ece_f506a1ddcd3eda6f3514f402fb138b41.png)
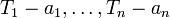
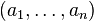
![\mathrm{Spm} k[T_1,\ldots, T_n]](https://static.techno-science.net/illustration/Definitions/autres/b/bed793fa82982acf98d36fe490759a48_3d0a061944fe20eb6fbfe4ebde11e3e2.png)
Si
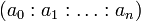
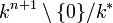
![k[T_0,\ldots, T_n]](https://static.techno-science.net/illustration/Definitions/autres/0/00e6a61cac2cd5cba01ea2bd98322bc8_294cfd9cfb599351a65892bf24662aa7.png)
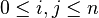
![k[T_0,\ldots, T_n]](https://static.techno-science.net/illustration/Definitions/autres/0/00e6a61cac2cd5cba01ea2bd98322bc8_294cfd9cfb599351a65892bf24662aa7.png)
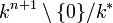
Soit
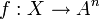
![A^n= \mathrm{Spm} k[T_1,\ldots, T_n]](https://static.techno-science.net/illustration/Definitions/autres/b/b03d3dd1f10d7659fd84a6eff62b8d9d_5b1c1a36ee81a1aba977c156e1cfe915.png)
![k[T_1, \ldots, T_n] \to O(X)](https://static.techno-science.net/illustration/Definitions/autres/4/4df84e48ab1f7edbafce758ae8ce6556_152f382e3ecd751924a13c3c3a5cb429.png)
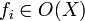
- Proposition. Pour tout point rationnel x de X, l'image f(x) est le point rationnel de An qui s'identifie à
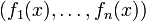
Corps particuliers
En géométrie algébrique réelle, on étudie les points réels
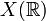

En géométrie algébrique complexe, on étudie surtout les points complexes
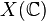
En géométrie arithmétique, le centre d'intérêt porte sur les points rationnels X(K) d'une variété algébrique définie sur un corps de nombres ou un corps fini K.
Immersions et sous-variétés
Une sous-variété ouverte d'une variété algébrique X est une partie ouverte U de X munie du faisceau de k-algèbres OX | U. Une sous-variété ouverte d'une variété algébrique est une variété algébrique. Une partie ouverte de X est toujours implicitement munie de cette structure de sous-variété ouverte.
On dit qu'un morphisme de variétés algébriques
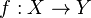
Toute variété affine est une sous-variété ouverte d'une variété projective.
On dit qu'un morphisme de variétés algébriques
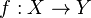
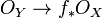
Une sous-variété fermée de X est une partie fermée Z de X munie d'une structure de variété algébrique de sorte que l'inclusion canonique
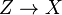
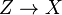
Toute partie fermée de X peut être munie d'une structure de sous-variété fermée (unique si on exige la sous-variété à être réduite).
On montre que toute sous-variété fermée d'une variété algébrique affine est affine, et que toute sous-variété fermée d'une variété projective est projective.
Une immersion de variétés algébriques est une composition (dans n'importe quel sens) d'une immersion ouverte et d'une immersion fermée. Une sous-variété est une sous-variété ouverte d'une sous-variété fermée (et aussi sous-variété fermée d'une sous-variété ouverte).
Une variété quasi-affine est une sous-variété d'une variété affine. Une variété quasi-projective est une sous-variété d'une variéte projective. Ainsi quasi-affine implique quasi-projective.

















































