Carré - Définition
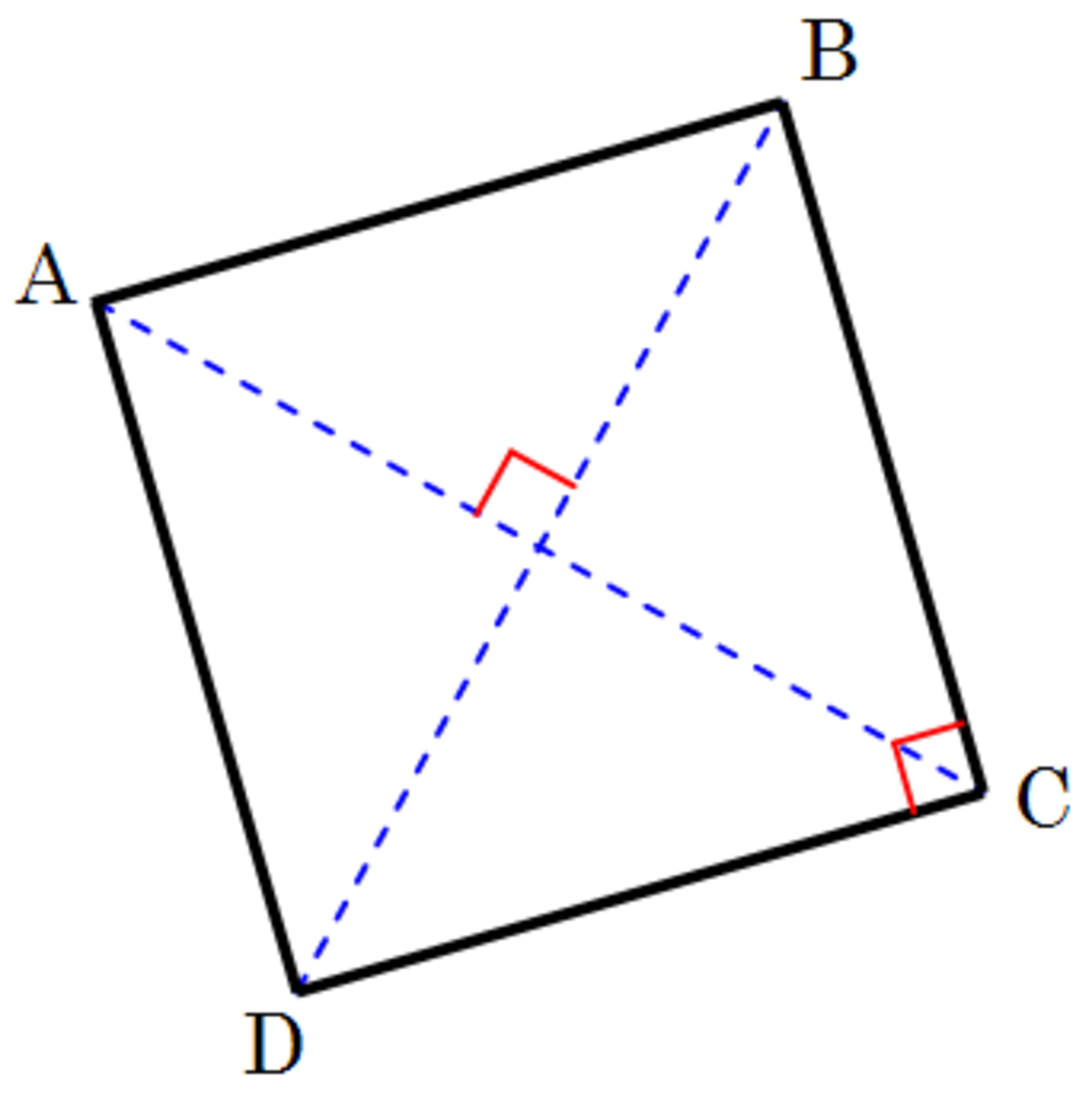
Un carré est un polygone régulier à quatre côtés : c'est un quadrilatère qui est à la fois un rectangle (il a quatre angles droits) et un losange (ses quatre côtés ont la même longueur).
Le terme " carré " désigne également l'élévation à la puissance 2 (sans doute en référence à la manière de calculer l'aire à partir du côté) : " a² " peut se lire " a au carré ". La courbe représentatrice de la fonction ƒ(x) = x² est une parabole.
Propriétés
Les quatre angles d'un carré sont droits.
Les diagonales d'un carré sont perpendiculaires et se coupent en leur milieu.
Les côtés opposés d'un carré sont parallèles deux à deux.
Soit "a" la longueur d'un côté d'un carré, alors la diagonale mesure a√2.
L'aire du carré est a².
Le triangle est invariant par rotation de centre O de π/4, π/2 (symétrie centrale) et 3π/4.
Le rectangle est invariant par symétrie axiale selon les bissectrices des côtés et selon les diagonales.
Toute droite passant par O divise le carré en deux parties superposables.
Il est aussi à noter que le carré possède les propriétés de tous les autres quadrilatères.
Construction
Construction au compas seul
On souhaite construire le carré de sommets ABCD connaissant seulement les points Aet B. Posons R la distance entre Aet B; alors, on procède comme suit:
- On trace C2 le cercle de centre Bet de rayon R (qui contient alors A)
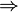
- Posons G un point d'intersection de C1 avec C2; on construit alors C3 centré en G et de rayon R. Ce cercle intersecte C1 en B et en un autre point H.
- C4, de centre H et de rayon R, intersecte C1 en G et en un nouveau point I.
- Posons S la distance entre G et I; on construit alors C5 de centre I et de rayon S (il contient forcément G).
- C6 s'obtient en prenant pour centre B et pour rayon S (il contient forcément H). On note J le point d'intersection entre C6 et C5 qui est du même côté que G par rapport à la droite AB.
- Si T est la distance entre A et J, on construit C7 le cercle de centre A et de rayon T (il contient forcément J).
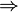
- On construit alors C8 de centre C et de rayon R.