Angle - Définition
La liste des auteurs de cet article est disponible ici.
Angles orientés de vecteurs
Rotations vectorielles
Rappelons à leur sujet deux points cruciaux pour la suite :
- Les isométries positives du plan sont celles des transformations préservant les longueurs dont le déterminant est 1. Ce sont les rotations vectorielles planes. Elles forment un sous-groupe SO(2) du groupe orthogonal O(2) du plan. SO(2) est commutatif comme U le groupe des nombres complexes de module 1, auquel il est isomorphe. L'exponentielle complexe permet alors de définir l'angle d'une rotation à
près.
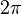
- Proposition.—Si u et v sont deux vecteurs unités distincts, il existe une unique rotation f envoyant u sur v. D'où une bijection T : (u,v) → f entre couples de vecteurs unitaires et rotations. Les vecteurs colonne de f forment alors la base orthonormalisée de Gram-Schmidt de la base (u,u').
Un angle orienté de vecteurs est une classe d'équivalence
- En disant que (u,v)R(u',v') s'il existe une rotation g telle que u'=g(u) et v'=g(v), on définit une relation d'équivalence R sur les couples de vecteurs unitaires. On appelle angle orienté de vecteurs les classes d'équivalence dans cette relation. En confondant abusivement un représentant et sa classe, on a par exemple : (-u,-v) = (u,v) par le demi-tour.
- La bijection T : (u, v)→ f « passe au quotient ». Précisément :
Théorème — l'angle orienté de vecteurs est caractérisé uniquement par la rotation associée. Formellement :
T(u,v) = T(u',v') si et seulement si (u,v)R(u',v').
Notons v=f(u), v'=g(u'), s(u)=u' et t(v)=v'.
- La rotation
envoie u sur u'. Elle est donc égale à la rotation s par unicité. On a donc tf = gs. Avec la commutativité de SO(2), on a f=g si et seulement si s=t qui est l'équivalence cherchée. CQFD
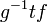
Si f=T(u,v) est une rotation d'angle 
, on dira aussi que est une mesure de l'angle orienté de vecteurs (u,v). Pour être digne d'un tel nom, il manque à cette mesure le caractère additif. Avec les angles géométriques, on a des ennuis additifs quand ils sont trop grands ! Pour les angles orientés de vecteurs, il faut d'abord définir la somme...
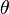
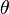
Les angles orientés de vecteurs forment un groupe
Somme d'angles orientés
La somme est définie en tirant en arrière le long de la bijection T la composition dans SO(2). En confondant un représentant avec sa classe, cela donne :
![(u,v)+(z,t) :=T^{-1} [T(u,v) \circ T(z,t)]](https://static.techno-science.net/illustration/Definitions/autres/8/84db98fb45b1662b4d0d54d97570dd59_d87c6290643619437da46d2d7f7d4309.png){kind=small}
- Le groupe des angles orientés de vecteurs est commutatif, comme SO(2).
- Avec T(u,v)oT(v,w)=T(u,w) on obtient pour les angles la relation de Chasles (u,v)+(v,w)=(u,w)
- L'angle plein correspond à l'identité : (u,u) = 0
- (v,u)+(u,v) = (v,v) = 0 et donc (v,u) est l'opposé de (u,v)
- L'angle plat est la moitié d'un plein : (-Id) o (-Id) = Id. L'angle plat s'écrit donc (u,-u).
- Il y a deux angles droits, solution de 2(u,v)=(u,-u)
Enfin une vraie mesure d'angles
- La mesure d'un angle orienté de vecteurs est définie par :
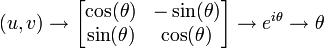
C'est un morphisme du groupe des angles orientés dans le groupe 
des réels muni de la somme modulo ; ainsi la mesure des angles est enfin additive !
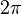
Effet des isométries sur les angles orientés de vecteurs
- Les isométries positives conservent les angles orientés de vecteurs par construction.
- Les réflexions orthogonales (isométries planes indirectes) renversent les angles orientés de vecteurs : si u et v sont deux vecteurs unitaires distincts, la réflexion s_D d'axe D dirigé par u+v échange u et v et donc (u,v) en son opposé(v,u). Toute réflexion s'obtient en composant s_D avec une rotation (on fait tourner l'axe) ; une telle réflexion renverse encore l'angle (u,v)