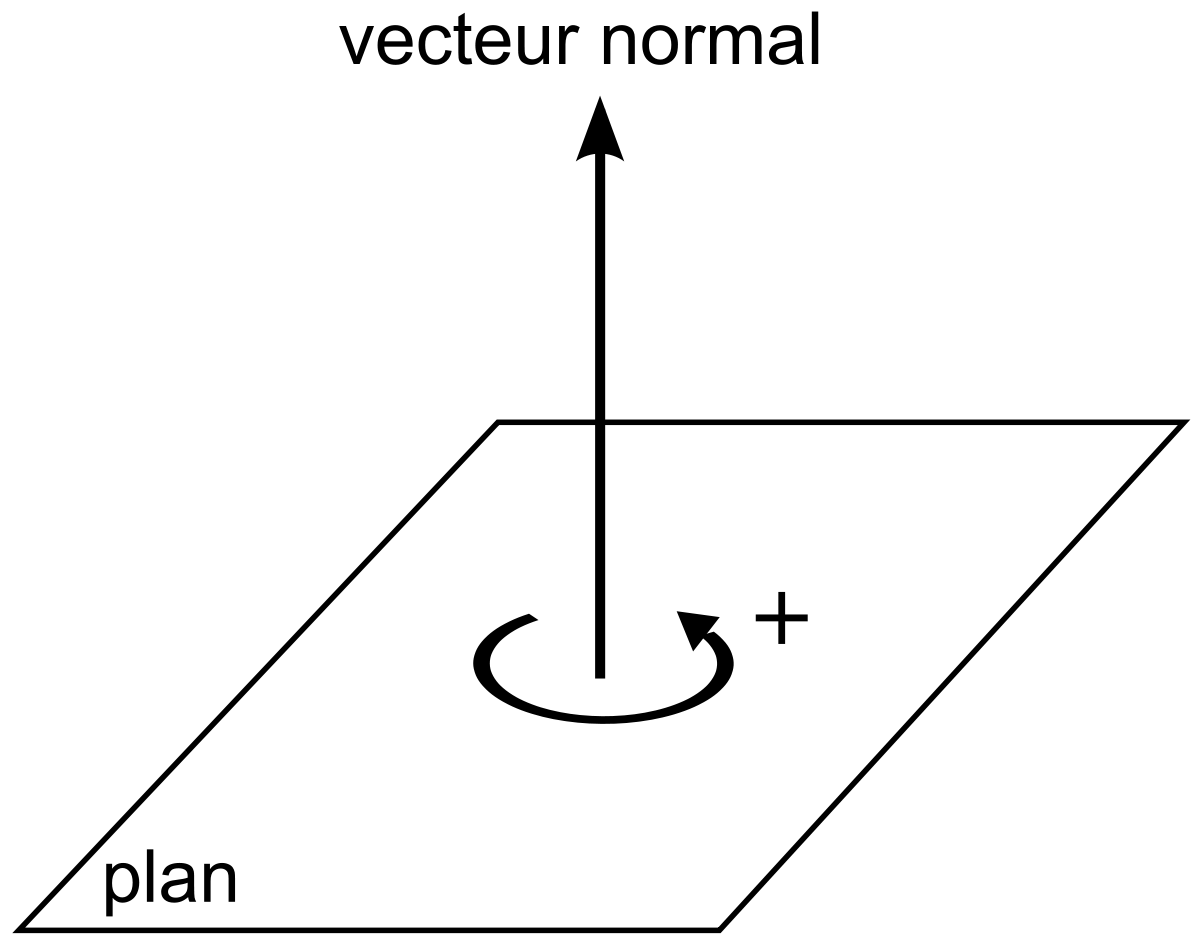
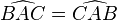Angle - Définition
La liste des auteurs de cet article est disponible ici.
Angles orientés dans le plan
Si le plan est orienté, alors les angles peuvent être positifs ou négatifs selon le sens dans lequel ils « tournent ».
-
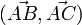
Par convention, on oriente le plan dans le sens dit « trigonométrique », c'est-à-dire dans le sens inverse des aiguilles d'une montre (ou « sens anti-horaire »). Si l'on considère deux demi-droites ou vecteurs, alors l'ordre dans lequel on cite les demi-droites ou les vecteurs définit le sens de l'angle, donc son signe ; ainsi :
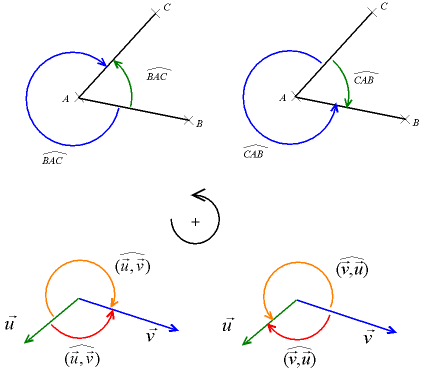
Les angles sont définis à un nombre entier de tours près. Ainsi, le plan complet peut être défini par un tour complet dans le sens positif, deux tours complets dans le sens positif, un tour complet dans le sens négatif... En radians, on dit que les angles sont définis à 2π près (« à deux pi près »). Par exemple, si l'angle α est droit de sens direct, il est noté :
ou bien
Cette dernière notation se lit : « alpha est congru à pi sur deux modulo deux pi ».
On remarque notamment que pour deux demi-droites (ou deux vecteurs) données, le fait de choisir la « petite » ou la « grande » portion de plan importe peu, puisque α ≡ α - 2π (cf. illustration ci-dessus).
Angle géométrique
Un angle géométrique est un objet mathématique pouvant être représenté par un secteur angulaire. On peut l'interpréter de plusieurs façons : divergence entre deux directions, directions des faces d'un objet (coin), direction visée par rapport au nord (angle donné par une boussole)…
-
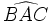
On a par ailleurs :
On confond fréquemment « mesure de l'angle » et « angle ». Ainsi par exemple un angle « plat » est appelé abusivement angle « égal » à 180.
Cet abus est appliqué largement et volontairement dans la suite de cet article.
D'autre part un angle droit par exemple, peut être représenté par plusieurs secteurs angulaires différents, mais comme ils sont tous « superposables », ils représentent tous le même angle. En mathématiques on parle de « classe d'équivalence ».
Ce problème se pose aussi lorsqu'on essaie de distinguer « fraction » et « rationnel ».
Angles dans l'espace
Deux droites sécantes sont nécessairement coplanaires, donc l'angle entre les droites est défini dans ce plan, de la même manière que ci-dessus. Pour orienter le plan, on choisit un vecteur normal au plan : le plan est alors orienté dans le sens trigonométrique lorsque le vecteur normal pointe vers l'observateur. Si l'on a défini une base
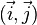
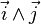
Pour définir l'angle entre deux plans, on considère l'angle que font leurs vecteurs normaux.
Pour définir l'angle entre un plan et une droite, on considère l'angle α entre la droite et sa projection orthogonale sur le plan, ou encore l'angle complémentaire entre la droite et la normale au plan : on retranche l'angle β entre la droite et la normale au plan de l'angle droit (α = π/2 - β en radians).
Pour définir l'angle entre deux droites quelconques de l'espace, on considère l'angle que font leurs vecteurs directeurs (dont le cosinus est égal au produit scalaire de ces vecteurs unitaires), ou encore l'angle planaire que fait une des deux droites avec une quelconque parallèle à l'autre qui la coupe. Cet angle est défini modulo les mêmes choix d'orientation évoqués ci-dessus.
On définit également les angles solides : on prend un point (parfois appelé « point d'observation ») et une surface dans l'espace (la « surface observée »), l'angle solide est la proportion de l'espace délimitée par le cône ayant pour sommet le point considéré et s'appuyant sur le contour de la surface. L'unité est le stéradian (sr en abrégé), l'espace complet fait 4π sr.
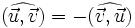
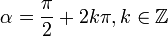
![\alpha \equiv \frac{\pi}{2} [2\pi]](https://static.techno-science.net/illustration/Definitions/autres/f/f31f734d59362ebfe8e8378214e8aa7a_33ae3f17c3c74e85883d6d0381629569.png)