Carte auto adaptative - Définition

Architecture

D'un point de vue architectural, les « cartes auto-organisatrices de Kohonen » sont constituées d'une grille (le plus souvent uni- ou bidimensionnelle). Dans chaque noeud de la grille se trouve un « neurone ». Chaque neurone est lié à un vecteur référent, responsable d'une zone dans l'espace des données (appelé encore espace d'entrée).

Dans une carte auto-organisatrice, les vecteurs référents fournissent une représentation discrète de l'espace d'entrée. Ils sont positionnés de telle façon qu'ils conservent la forme topologique de l'espace d'entrée. En gardant les relations de voisinage dans la grille, ils permettent une indexation facile (via les coordonnées dans la grille).
Ceci s'avère utile dans divers domaines, comme la classification de textures, l'interpolation entre des données, la visualisation des données multidimensionnelles.

Soit A la grille neuronale rectangulaire d'une carte auto-organisatrice. Une carte de neurones assigne à chaque vecteur d'entrée un neurone désigné par son vecteur de position , tel que le vecteur référent w_r est le plus proche de v.

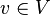
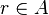
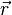
Mathématiquement, on exprime cette association par une fonction:

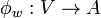
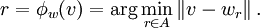
Cette fonction permet de définir les applications de la carte.

• quantificateur vectoriel: on approxime chaque point dans l'espace d'entrée par le vecteur référent le plus proche par

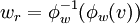
• classificateur en utilisant la fonction r = φ_w(v)

on assigne à chaque neurone de la grille une étiquette correspondante à une classe; tous les points de l'espace d'entrée qui se projettent sur un même neurone appartiennent à la même classe. Une même classe peut être associée à plusieurs neurones.

Avantages et inconvénients des cartes auto adaptatives

Les ancêtres des cartes auto-organisatrices, les algorithmes comme "k-moyennes", réalisent la discrétisation de l'espace d'entrée en ne modifiant à chaque cycle d'adaptation qu'un seul vecteur référent. Leur processus d'apprentissage est donc très long.

L'algorithme de Kohonen profite des relations de voisinage dans la grille pour réaliser une discrétisation dans un temps très court. On suppose que l'espace n'est pas constitué de zones isolées, mais de sous-ensembles compacts.
Donc en déplaçant un vecteur référent vers une zone, on peut se dire qu'il y a probablement d'autres zones dans la même direction qui doivent être représentées par des vecteurs référents. Cela justifie le fait de déplacer les neurones proches du vainqueur dans la grille dans cette même direction, avec une amplitude de déplacement moins importante. L'algorithme présente des opérations simples ; il est donc très léger en terme de coût de calculs.

Le voisinage dans les cartes auto adaptatives est malheureusement fixe, et une liaison entre neurones ne peut être cassée même pour mieux représenter des données discontinues. Les Growing Cell Structure, ou Growing Neural Gas sont la solution à ce problème. Des neurones et les liaisons entre neurones peuvent y être supprimées ou ajoutées quand le besoin s'en fait sentir.

Propriétés

• Similitude des densités dans l'espace d'entrée
  La carte reflète la distribution des points dans l'espace d'entrée. Les zones dans lesquelles les vecteurs d'entraînement v sont tirés avec une grande probabilité d'occurrence sont cartographiées avec une meilleure résolution que les zones

dans lesquelles les vecteurs d'entraînement v sont tirés avec une petite probabilité d'occurrence.

• Préservation des relations topologiques :
  des neurones voisins dans la grille occupent des positions voisines dans l'espace d'entrée (préservation des voisinages de la grille) ; et des points

proches dans l'espace d'entrée se projettent sur des neurones voisins dans la grille (préservation de la topologie de l'espace d'entrée). Les neurones ont tendance à discrétiser l'espace de façon ordonnée.