Topologie - Définition

Introduction

un ruban de Möbius est une surface fermée dont le bord se réduit à un cercle. De tels objets sont des sujets étudiés par la topologie.

La topologie est une branche des mathématiques concernant l'étude des déformations spatiales par des transformations continues (sans arrachages ni recollement des structures). Pour la structure formelle de topologie, voir Espace topologique.

Étymologie

Le mot « topologie » vient de la contraction des noms grecs topos et logos qui signifient respectivement « lieu » et « étude ». Littéralement, la topologie signifie l'« étude du lieu ». Elle s’intéresse donc à définir ce qu’est un lieu (appelé aussi « espace ») et quelles peuvent en être les propriétés. Une ancienne dénomination fut analysis situs, c'est-à-dire « l'étude du lieu ».

La topologie s’intéresse plus précisément aux espaces topologiques et aux applications qui les lient, dites « continues ».

Elle permet de classer ces espaces, notamment les nœuds, entre autres par leur dimension (qui peut être aussi bien nulle qu’infinie).

Elle s’intéresse aussi à leurs déformations.

En analyse, grâce aux informations qu’elle fournit sur l’espace considéré, elle permet d’obtenir un certain nombre de résultats (existence et/ou unicité de solutions d’équations différentielles, notamment).

Les espaces métriques ainsi que les espaces vectoriels normés sont des exemples d’espaces topologiques.

Branches de la topologie

• Topologie générale

La topologie générale étudie les notions fondamentales de la topologie. On y recherche la plus grande simplicité et la plus grande généralité. Cela oblige à une certaine abstraction.

Pour comprendre les notions abstraites de la topologie générale, il est nécessaire de connaitre déjà de nombreux exemples issus de la géométrie ou de l'analyse. Limite d'une suite, limite d'une fonction, convexité, distance sont des notions qui permettent d'entrer dans la théorie.

• Topologie algébrique

L'idée de la topologie algébrique consiste à associer à différents espaces des invariants de manière à pouvoir les classifier. Les premiers invariants découverts étaient numériques. Aujourd'hui ces invariants sont des structures algébriques, groupes, anneaux, le plus souvent. Les correspondances entre espaces et objets sont des foncteurs et la théorie des catégories simplifie parfois la compréhension de celles-ci.

Citons entre autres, le groupe fondamental et l'homologie singulière.

• Géométrie différentielle

La géométrie différentielle étudie les variétés différentielles ainsi que leurs plongements dans des espaces euclidiens.

Principes fondateurs

Le concept central en topologie est la notion de limite. Prenons l'exemple d'une surface fermée, un disque par exemple. D'un strict point de vue ensembliste, il y a les points qui sont dans le disque et ceux qui ne sont pas dedans. Pourtant, ce point de vue n'est pas satisfaisant géométriquement. Les points qui sont sur le cercle délimitant le disque ont un statut particulier, ils sont à la limite. D'ailleurs, au moment de la définition d'un disque, on a un choix à faire : Quand on parle du disque, considère-t-on l'ensemble des points dont la distance au centre est inférieure ou égale au rayon ou considère-t-on l'ensemble des points dont la distance au centre est strictement inférieure au rayon ? Dans le premier cas, on dit que le disque est fermé, dans le second cas, on dira que le disque est ouvert. Plus généralement, on dira qu'une surface est fermée lorsqu'elle contient tous ses points limites et qu'elle est ouverte si elle n'en contient aucun.

Cette idée de limite est très visuelle. La topologie va chercher à formaliser cette notion. Il y a plusieurs moyens d'y parvenir. La façon la plus simple est de définir une distance. Dans notre exemple, on utilise simplement la distance euclidienne. Les points limites sont ceux qui sont proches (c'est-à-dire à une distance aussi faible que désirée) à la fois de points dans notre surface et de points qui ne sont pas dedans. Définir une distance sur un ensemble lui confère une structure d'espace métrique. Cette façon de voir est suffisante pour résoudre de nombreux problèmes. Cependant, utiliser une distance passe par l'intermédiaire des nombres réels et introduit donc une contrainte qu'il a fallu dépasser. Pour cela, on a été amené à définir le concept de proximité de façon plus abstraite, sans faire appel à un argument numérique, c'est le concept de voisinage. Pour des raisons techniques, il est équivalent et plus simple de définir directement les ouverts avant les voisinages, c'est donc ainsi que l'on définit usuellement une topologie : en décidant quelles sont les parties ouvertes.

La notion de limite n'est pas seulement statique mais aussi dynamique. La topologie permet d'appréhender les limites de fonctions ou de suites. Regardons la suite des inverses des nombres entiers à partir de 1 : . A la limite, cette suite va tendre vers 0. Cela rejoint plus ou moins le fait que 0 est un point limite de l'ensemble des .

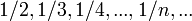
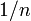
Il est important de noter que la plupart des notions de topologie, notamment la continuité sont des conséquences de la notion de limite. C'est le cas notamment de la notion de dérivée qui se conçoit comme limite du taux d'acroissement, de la tangente qui est la limite des cordes.

La topologie est donc une théorie très unificatrice : elle explique avec très peu d'axiomes initiaux un grand nombre de phénomènes.