Probabilité - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La probabilité (du latin probabilitas) est une évaluation du caractère probable d'un évènement. En mathématiques, l'étude des probabilités est un sujet de grande importance donnant lieu à de nombreuses applications.
La probabilité d'un événement est un nombre réel compris entre 0 et 1. Plus ce nombre est grand, plus le risque (ou la chance, selon le point de vue) que l'événement se produise est grand. Si on considère que la probabilité qu'un lancer de pièce donne pile est égale à 1/2, cela signifie que, si on lance un très grand nombre de fois cette pièce, la fréquence des piles va tendre vers 1/2, sans préjuger de la régularité de leur répartition. Cette notion empirique sera définie plus rigoureusement dans le corps de cet article.
Contrairement à ce que l'on pourrait penser de prime abord l'étude scientifique des probabilités est relativement récente dans l'histoire des mathématiques. D'autres domaines tels que la géométrie, l'arithmétique, l'algèbre ou l'astronomie faisaient l'objet d'étude mathématique durant l'Antiquité mais on ne trouve pas de trace de textes mathématiques sur les probabilités. L'étude des probabilités a connu de nombreux développements au cours des trois derniers siècles en partie grâce à l'étude de l'aspect aléatoire et en partie imprévisible de certains phénomènes, en particulier les jeux de hasard. Ceux-ci ont conduit les mathématiciens à développer une théorie qui a ensuite eu des implications dans des domaines aussi variés que la météorologie, la finance ou la chimie. Cet article est une approche simplifiée des concepts et résultats d'importance en probabilité ainsi qu'un historique de l'usage du terme "probabilité" qui a eu plusieurs autres sens avant celui qu'on lui connaît aujourd'hui en mathématiques.
Histoire
A l'origine, dans les traductions d'Aristote, le mot "probabilité" ne désigne pas une quantification du caractère aléatoire d'un fait mais l'idée qu'une idée est communément admise par tous. Ce n'est que au cours du Moyen Âge puis de la Renaissance autour des commentaires successifs et des imprécisions de traduction de l'œuvre d'Aristote que ce terme connaîtra un glissement sémantique pour finir par désigner la vraisemblance d'une idée. Au XVIe siècle puis au XVIIe siècle c'est ce sens qui prévaut en particulier dans le probabilisme en théologie morale. C'est dans la deuxième moitié du XVIIe siècle, à la suite des travaux de Blaise Pascal, Pierre de Fermat et Christian Huygens sur le problème des partis que ce mot prend peu à peu son sens actuel avec les développements du traitement mathématique du sujet par Jakob Bernoulli . Ce n'est alors qu'au XIXe siècle qu'apparaît ce qui peut être considéré comme la théorie moderne des probabilités en mathématiques.
La notion de probabilité chez Aristote
Le premier usage du mot probabilité apparait en 1370 avec la traduction de l'éthique à Nicomaque d'Aristote par Oresme et désigne alors « le caractère de ce qui est probable ». Le concept de probable chez Aristote (ενδοξον, en grec) est ainsi défini dans les Topiques :
"Sont probables les opinions qui sont reçues par tous les hommes, ou par la plupart d’entre eux, ou par les sages, et parmi ces derniers, soit par tous, soit par la plupart, soit enfin par les plus notables et les plus illustres"
Ce qui rend une opinion probable chez Aristote est son caractère généralement admis; ce n'est qu'avec la traduction de Cicéron des Topiques d'Aristote, qui traduit par probabilis ou par verisimilis, que la notion de vraisemblance est associée à celle de "probabilité" ce qui aura un impact au cours du Moyen Âge puis de la Renaissance avec les commentaires successifs de l'œuvre d'Aristote.
La doctrine de la probabilité au XVIe siècle et XVIIe siècle
La doctrine de la probabilité, autrement appelée probabilisme, est une théologie morale catholique qui s'est développée au cours du XVIe siècle sous l'influence entre autres de Bartolomé de Medina et des jésuites. Avec l'apparition de la doctrine de la probabilité, ce terme connaîtra un glissement sémantique pour finir par désigner au milieu du XVIIe siècle le caractère vraisemblable d'une idée.
Cette théologie morale considère que "si une opinion est probable, il est permis de la suivre, quand bien même est plus probable l’opinion opposée" selon la formulation de Bartolomé de Medina en 1527. Cette théologie morale cherche alors à définir quelle action entreprendre quand il existe un doute sur la meilleure action à entreprendre. Cette théologie morale a été très critiquée à partir du milieu du XVIIe siècle comme introduisant le relativisme moral, en particulier par les jansénistes et par Blaise Pascal, qui sera, par ailleurs, l'un des fondateurs du traitement mathématique du probable..
La probabilité d'une opinion désigne alors au milieu du XVIIe siècle la probabilité qu'une opinion soit vraie. Ce n'est qu'à partir de la fin du XVIIe siècle avec l'émergence de la probabilité mathématique que la notion de probabilité ne concernera plus seulement les opinions et les idées mais aussi les faits et se rapprochera de la notion de hasard que l'on connaît aujourd'hui.
La notion moderne de probabilité
L'apparition de la notion de "risque", préalable à l'étude des probabilités, n'est apparue qu'au XIIe siècle pour l'évaluation de contrats commerciaux avec le Traité des contrats de Pierre de Jean Olivi, et s'est développée au XVIe siècle avec la généralisation des contrats d'assurance maritime. À part quelques considérations élémentaires par Girolamo Cardano au début du XVIe siècle et par Galilée au début du XVIIe siècle, le véritable début de la théorie des probabilités date de la correspondance entre Pierre de Fermat et Blaise Pascal en 1654.
Ce n'est qu'à partir du milieu du XVIIe siècle avec l'émergence du traitement mathématique du sujet qu'est apparu l'usage moderne du terme probabilité.
Les probabilités du XVIIe au XIXe siècle
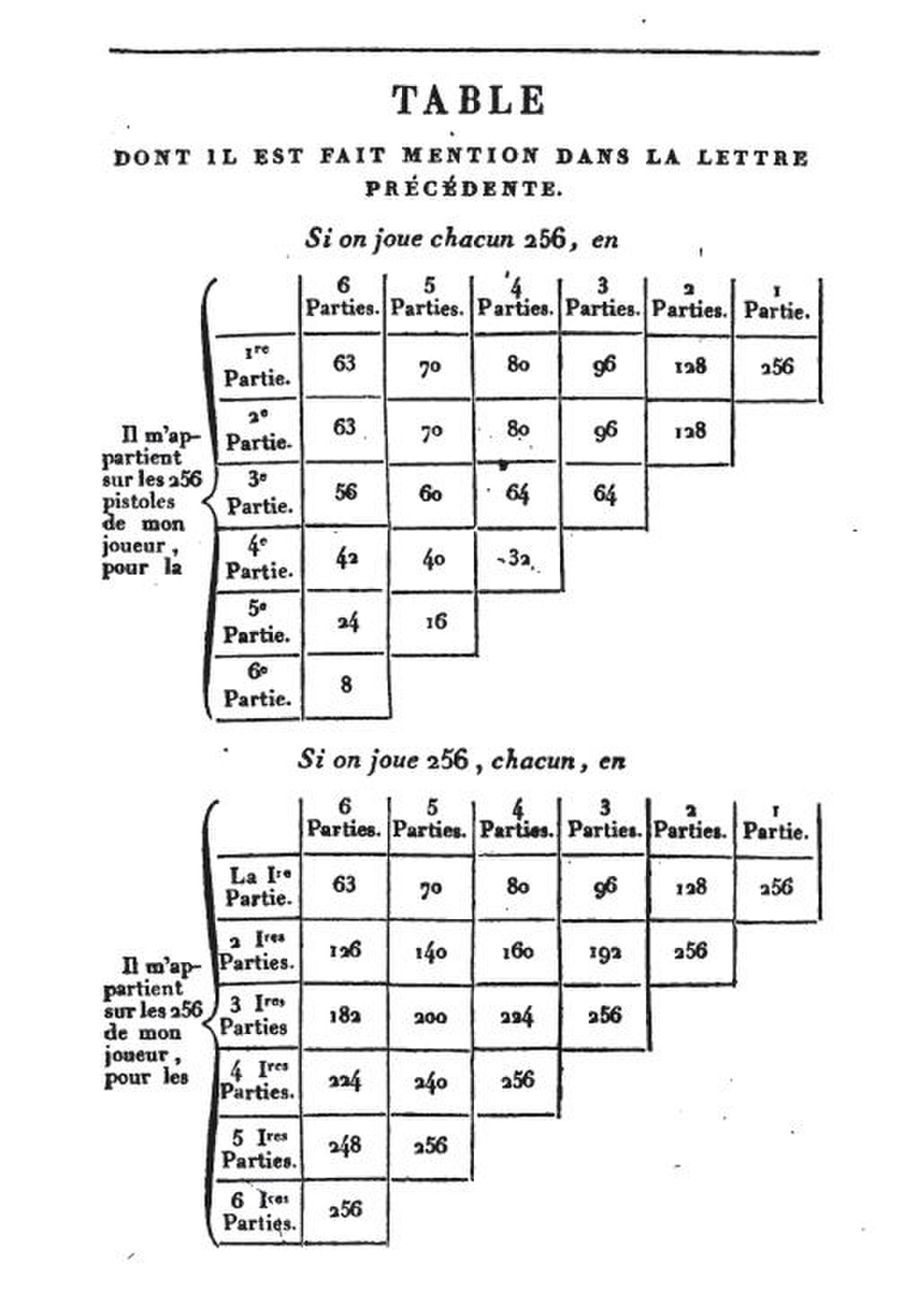
Le véritable début de la théorie des probabilités date de la correspondance entre Pierre de Fermat et Blaise Pascal en 1654. Ceux-ci commencent à élaborer les bases du traitement mathématique des probabilités autour de l'étude de jeux de hasard proposés, entre autres, par le chevalier de Méré. (voir ci-contre une page de la correspondance entre Pascal et Fermat au sujet du problème des partis). Même s'ils sont considérés comme les fondateurs du traitement des probabilités, ils n'ont rien publié de leurs travaux, et il faudra attendre Huygens pour avoir un premier ouvrage sur le sujet.
Encouragé par Pascal, Christian Huygens publie De ratiociniis in ludo aleae (raisonnements sur les jeux de dés) en 1657. Ce livre est le premier ouvrage important sur les probabilités. Il y définit la notion d'espérance et y développe plusieurs problèmes de partages de gains lors de jeux ou de tirages dans des urnes. Deux ouvrages fondateurs sont également à noter : Ars Conjectandi de Jacques Bernoulli (posthume, 1713) qui définit la notion de variable aléatoire et donne la première version de la loi des grands nombres, et Théorie de la probabilité d' Abraham de Moivre (1718) qui généralise l'usage de la combinatoire.
La Théorie des erreurs, qui cherche à quantifier l'écart entre la mesure que l'on fait d'une variable et sa vraie valeur et qui est une préfiguration des théorèmes central limite, voit le jour avec Opera Miscellanea de Roger Cotes (posthume, 1722). Le premier à l'appliquer aux erreurs sur les observations est Thomas Simpson en 1755.
Pierre-Simon de Laplace donne une première version du théorème central limite en 1812 qui ne s'applique alors que pour une variable à deux états, par exemple pile ou face mais pas un dé à 6 faces.
Sous l'impulsion de Quetelet, qui ouvre en 1841 le premier bureau statistique le Conseil Supérieur de Statistique, les statistiques se développent et deviennent un domaine à part entière des mathématiques qui s'appuie sur les probabilités mais n'en font plus partie.
Naissance de la théorie classique des probabilités
La théorie de la probabilité classique ne prend réellement son essor qu'avec les notions de mesure et d'ensembles mesurables qu'Émile Borel introduit en 1897. Cette notion de mesure est complétée par Henri Léon Lebesgue et sa théorie de l'intégration. La première version moderne du théorème de la limite centrale est donné par Alexandre Liapounov en 1901 et la première preuve du théorème moderne est donnée par Paul Lévy en 1910. En 1902, Andrei Markov introduit les chaînes de Markov pour entreprendre une généralisation de la loi des grands nombres pour une suite d'expériences dépendant les unes des autres. Ces chaînes de Markov connaîtront de nombreuses applications entre autres pour modéliser la diffusion ou pour l'indexation de sites internet sur Google.
Il faudra attendre 1933 pour que la théorie des probabilités sorte d'un ensemble de méthodes et d'exemples divers et devienne une véritable théorie, axiomatisée par Kolmogorov.
Kiyoshi Itô met en place une théorie et un lemme qui porte son nom dans les années 1940. Ceux-ci permettent de relier le calcul stochastique et les équations aux dérivées partielles faisant ainsi le lien entre analyse et probabilités. Le mathématicien Wolfgang Doeblin avait de son côté ébauché une théorie similaire avant de se suicider à la défaite de son bataillon en juin 1940. Ses travaux furent envoyés à l'Académie des sciences dans un pli cacheté qui ne fut ouvert qu'en 2000.