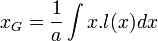Centre de masse d'une plaque homogène - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Calcul intégral
Si l'on munit la plaque d'un repère orthonormé, l'abscisse et l'ordonnée du centre de masse peuvent être calculées à l'aide d'un calcul intégral. Si l'on appelle l(x) la longueur totale de la section de la plaque par la droite d'abscisse x, et si a est l'aire de la plaque, l'abscisse du centre de masse est donné par la formule