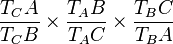Cercles inscrit et exinscrits d'un triangle - Définition

Cercle inscrit

Il existe un et un seul cercle intérieur au triangle et tangent à la fois à ses trois côtés. Ce cercle de centre est appelé « cercle inscrit » dans le triangle.

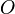
Le cercle inscrit à un triangle est le plus grand cercle que peut contenir ce triangle. Son centre est le barycentre des points (A,a) (B,b) (C,c). Son rayon est égal à

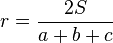
où S désigne la surface du triangle. Son centre est le point d'intersection des bissectrices.

Point de Gergonne

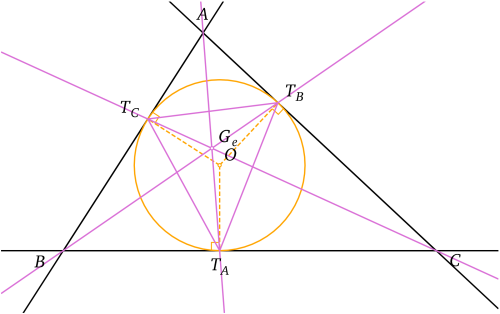
Notons respectivement T_A, T_B et T_C les points de contact du cercle inscrit avec les côtés [BC], [AC] et [AB]. Alors les droites (AT_A), (BT_B) et (CT_C) sont concourantes : en effet, le produit des rapports

est égal à 1 grâce aux égalités

T_CA = T_BA, T_BC = T_AC, T_AB = T_CB.

D'après le théorème de Ceva ces trois céviennes sont concourantes en un point qui s'appelle le point de Gergonne du triangle et le triangle T_AT_BT_C s'appelle le triangle de Gergonne du triangle ABC.

Point de Gergonne d'un triangle.

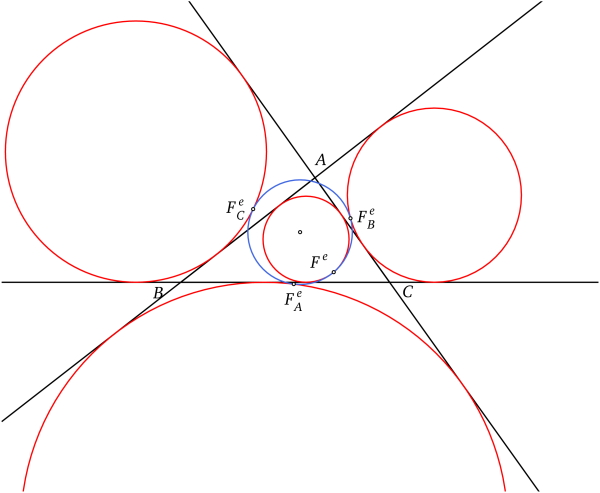
Théorème de Feuerbach

Les trois cercles exinscrits et le cercle inscrit sont tangents au cercle d'Euler du triangle. Les points de contact de ces cercles s'appellent les points de Feuerbach du triangle. Ce résultat constitue le théorème de Feuerbach.

Les trois points de tangence des cercles exinscrits forment le triangle de Feuerbach du triangle.

Triangle de Feuerbach.