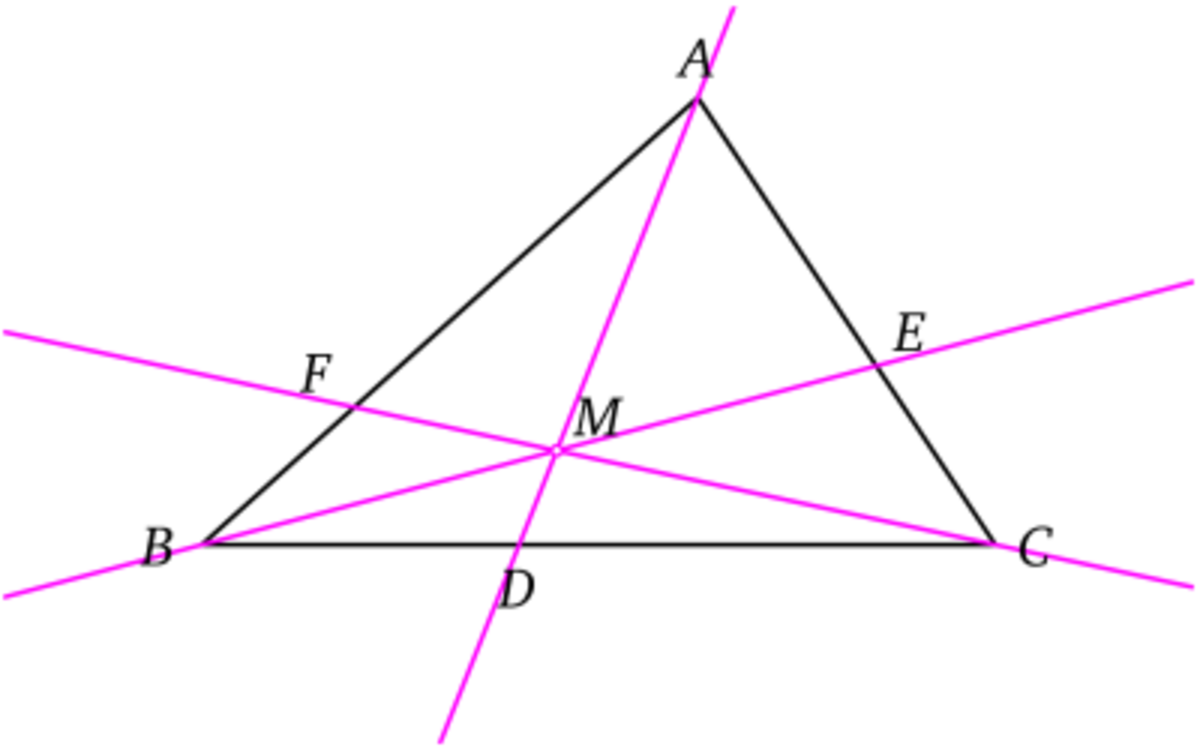
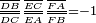Théorème de Ceva - Définition

Introduction

Les droites (AD), (BE) et (CF) sont concourantes ou parallèles si et seulement si .

En mathématiques, le théorème de Ceva est un théorème de géométrie affine plane qui donne une condition nécessaire et suffisante pour que trois droites passant par les trois sommets d'un triangle soient parallèles ou concourantes. Il s'interprète naturellement en géométrie euclidienne et se généralise en géométrie projective.

Il doit son nom au mathématicien italien Giovanni Ceva qui, quelques années après le mathématicien espagnol José Zaragoza, en énonce et démontre une version dans le De lineis rectis se invicem secantibus statica constructio en 1678. Cependant, il était déjà connu, à la fin du XI^e siècle, de Yusuf Al-Mu'taman ibn Hűd, géomètre et roi de Saragosse. Celui-ci le démontre dans son Livre de perfection (Kitab al-Istikmal), célèbre en son temps mais dont le texte n'a été redécouvert qu'en 1995.

Géométrie euclidienne

Cette section présente un cas particulier du théorème de Ceva, celui où les trois droites passant par chacun des sommets du triangle sont intérieures à celui-ci. L'énoncé se simplifie : ces trois droites ne peuvent être parallèles, et il suffit de parler de rapports de longueurs.

Énoncé avec des distances

Théorème — Soit ABC un triangle, soient D, E et F trois points distincts des sommets et appartenant respectivement aux segments [BC], [CA] et [AB]. Les droites (AD), (BE) et (CF) sont concourantes si et seulement si

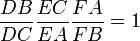
On appellera dans la suite cévienne d'un triangle une droite passant par un sommet et rencontrant le segment opposé. Ici, les points D, E et F sont bien sur les côtés.

On va donner une démonstration ne faisant intervenir que des notions de proportionnalité de longueurs et d'aires, des outils qui étaient déjà disponibles à l'époque d'Euclide.

Démonstration — On note dans la suite A_ABC l'aire du triangle ABC et on démontre la propriété en deux temps.

Si les droites sont concourantes en M alors le produit des rapports vaut 1.

Les triangles MDB et MDC ayant même hauteurs, leur aires sont proportionnelles aux bases DB et DC. De même pour les triangles ADB et ADC, puis par différence pour les triangles MAB et MAC. On obtient donc l'égalité

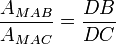
Par un raisonnement analogue, on a et

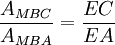
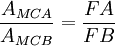
Le produit des trois rapports est bien égal à 1

Si le produit des rapports est 1 alors les droites sont concourantes

Les droites étant des céviennes, les droites (AD) et (BE) se coupent en M et la droite (CM) coupe [AB] en F'

D'après le raisonnement précédent, on a

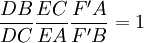
Comme il vient par simplification que . Or il n'existe qu'un seul point sur un segment qui divise celui-ci selon un rapport donné donc F = F'. La droite (CF) passe aussi par M.

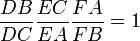
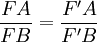
Énoncé sous forme trigonométrique

On peut déduire du théorème de Ceva par la loi des sinus une version trigonométrique de celui-ci.

Théorème — Soit ABC un triangle, soient D, E et F trois points distincts des sommets et appartenant respectivement aux segments [BC], [CA] et [AB]. Les droites (AD), (BE) et (CF) sont concourantes si et seulement si

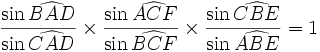
En géométrie projective

Dans le plan projectif, toutes les droites sont sécantes. On peut construire le plan projectif en ajoutant une droite, dite droite à l'infini, au plan affine. Les droites du plan affine d'une même direction sont sécantes en un même point (dit parfois point impropre) sur cette droite à l'infini. Il devient inutile de distinguer deux cas dans l'énoncé du théorème. Par contre les rapports de mesures algébriques ne sont pas des notions projectives. On peut parler de birapport : Dans la construction du plan projectif comme complété du plan affine, le birapport [A,B,C,D] égale le rapport de la mesure algébrique de [CA] sur celle de [CB] quand D est à l'infini. On peut aussi donner une version du théorème en coordonnées homogènes, qui sont l'extension des coordonnées barycentriques au plan projectif.