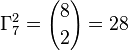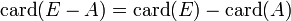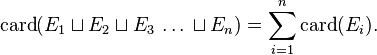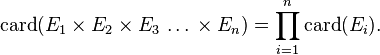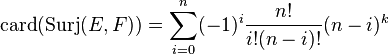Combinatoire - Définition

Dénombrement

Dans cette section, si A est un ensemble fini, on note card(A) (lire « cardinal de A ») le nombre de ses éléments. Par exemple, card({e,f,g}) = 3.

• Si A et B sont deux parties d'un ensemble fini, alors

.

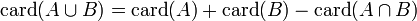
• Si A est une partie d'un ensemble fini E alors

Soient E et F deux ensembles finis avec E de cardinal k et F de cardinal n.

• La somme disjointe est finie de cardinal

.

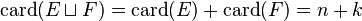
Plus généralement, pour une suite d'ensembles disjoints deux à deux,

• Le produit cartésien est fini de cardinal

.

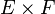
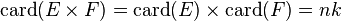
Plus généralement, pour une suite d'ensembles finis,

• L'ensemble des parties de E, qui est en correspondance biunivoque avec l'ensemble des applications de E dans , est donc fini et de cardinal

.

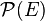
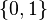
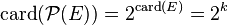
• L'ensemble des correspondances de E dans F, noté habituellement Corr(E,F), s'identifie à donc est fini de cardinal

.

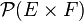
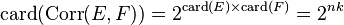
• L'ensemble des applications de E dans F, souvent noté est fini de cardinal

.

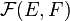
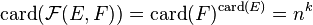
avec la convention 0⁰=1 si E et F sont tous deux vides.

Cette propriété justifie la notation plus courante F^E.

• L'ensemble des surjections de E dans F, noté habituellement Surj(E,F), est vide si card(E) < card(F). Dans le cas contraire,

Les applications injectives, qui jouent un rôle important en combinatoire, sont traitées de manière plus approfondie dans les paragraphes suivants.

Combinaisons (choix sans tenir compte de l'ordre)

Contrairement aux arrangements, les combinaisons sont des dispositions d'objets qui ne tiennent pas compte de l'ordre de placement de ces objets. Par exemple, si a, b et c sont des boules tirées d'une urne, abc et acb correspondent au même tirage. Il y a donc moins de combinaisons que d'arrangements.

Combinaisons sans répétition

Si nous tirons sans remise k objets parmi n objets discernables, et nous les disposons sans tenir compte de l'ordre d'apparition, nous pouvons représenter ces k objets par une partie à k éléments d'un ensemble à n éléments. Ce sont des combinaisons sans répétition de n éléments pris k à k.

Pour déterminer le nombre de ces dispositions, nous pouvons déterminer le nombre d'arrangements de k objets et diviser par le nombre de dispositions obtenues les unes à partir des autres par une permutation. Il y en a (pour la notation, voir aussi l'article sur le coefficient binomial).

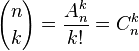
Par exemple le jeu Euromillions demande de choisir 5 nombres différents entre 1 et 50 et 2 nombres entre 1 et 9, soit possibilités.

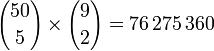
Combinaisons avec répétition

Si nous tirons avec remise k objets parmi n objets discernables, et nous les disposons sans tenir compte de l'ordre d'apparition; ces objets peuvent apparaître plusieurs fois et nous ne pouvons les représenter ni avec une partie à k éléments, ni avec un k-uplet puisque leur ordre de placement n'intervient pas. Il est cependant possible de représenter de telles dispositions avec des applications appelées combinaisons avec répétition.

Le nombre de combinaisons avec répétition de n éléments pris k à k est égal à : .

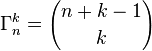
Donnons l'exemple du jeu de domino. Les pièces sont fabriquées en disposant côte à côte deux éléments de l'ensemble {blanc, 1, 2, 3, 4, 5, 6}. Si nous retournons un domino, nous changeons l'ordre des deux éléments, mais le domino reste identique. Nous avons une combinaison avec répétition de 7 éléments pris 2 à 2, et au total il y a : dominos dans un jeu.