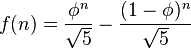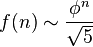Combinatoire - Définition

Arrangements (choix en tenant compte de l'ordre)

Arrangements sans répétition

Nous disposons de n objets discernables et nous voulons en placer k, en tenant compte de l'ordre, dans k cases numérotées de 1 à k avec un et un seul objet par case. Le nombre de dispositions est alors égal au nombre de k-listes distinctes formées à partir de ces objets. Au lieu de constituer un n-uplet, à partir de n objets discernables, nous formons ici des k-uplets avec à partir de ces n objets tels que pour , on ait . Un tel k-uplet s'appelle un arrangement sans répétition de n éléments pris k à k.

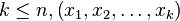
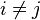
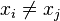
Théorème 

Le nombre d'arrangements sans répétition de n éléments pris k à k est égal à (égal à si k≤n et à 0 sinon).

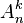
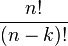
En effet, Il y a n choix possibles de l'objet qui occupe la première place du k-uplet, n-1 choix pour l'objet de la 2^e place ; pour la k^e, il ne reste plus que n-(k-1) objets et donc n-k+1 choix possibles. Le produit s'écrit bien sous la forme : . C'est juste le nombre des injections de l'ensemble {1,2, ..., k} dans l'ensemble {1,2, ..., n}.

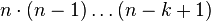
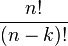
Le cas n = k nous oblige alors à diviser par (0)! que l'on définit comme valant 1.

Arrangements avec répétition

Lorsque nous voulons placer des objets pris parmi n objets discernables dans k emplacements en tenant compte de l'ordre, ces objets pouvant apparaître plusieurs fois, le nombre de dispositions est alors égal au nombre de k-uplets formés à partir de ces n objets. Un tel k-uplet, avec k≤n, (x₁, x₂, …, x_k) formé à partir de ces n objets s'appelle un arrangement avec répétition de n éléments pris k à k.

Comme chaque emplacement peut être occupé indifféremment par l'un quelconque de ces n objets, il y en a au total n^k.

Quand nous tirons 11 fois l'un de 3 numéros en tenant compte de l'ordre d'apparition nous obtenons au total 3¹¹ = 177 147 tirages différents. Comme exemple tiré de la génétique, nous pouvons donner le nombre total de codons de base (triplets formés de quatre codes) : 4³= 64.

Quelques résultats

Un théorème, dû à Franck P. Ramsey, donne un résultat surprenant. À une soirée à laquelle se rendent au moins six personnes, il y a au moins trois personnes qui se connaissent mutuellement ou au moins trois qui sont étrangères les unes aux autres.

Démonstration 

soit P₁ une personne quelconque présente à la soirée. Sur les n-1 autres, soit elle en connaît au plus deux, soit elle en connaît au moins trois. Supposons que l’on est dans le second cas, et soient trois personnes connues de P₁. Si deux d’entre elles se connaissent, mettons P₂ et P₃, alors se connaissent toutes trois. Sinon, ne se connaissent pas du tout, et le résultat annoncé est encore juste. Dans l’autre cas de figure (P₁ connaît au plus deux personnes du groupe), le même raisonnement, inversé, fonctionne avec les trois personnes que P₁ ne connaît pas.

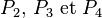
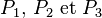
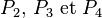
(C'est un cas particulier du théorème de Ramsey.)

L'idée de trouver un ordre dans des configurations aléatoires mène à la théorie de Ramsey. Essentiellement, cette théorie indique que n'importe quelle configuration suffisamment grande contiendra au moins un autre type de configuration.

Fonction de comptage

Soit S_n l'ensemble des permutations de {1, 2, …, n}. Nous pouvons considérer la fonction qui à n associe le nombre de permutations. Cette fonction est la fonction factorielle et sert à compter les permutations.

Étant donnée une collection infinie d'ensembles finis indexée par l'ensemble des entiers naturels, une fonction de comptage est une fonction qui à un entier n associe le nombre d'éléments de E_n. Une fonction de comptage f permet donc de compter les objets de E_n pour n'importe quel n. Les éléments de E_n ont habituellement une description combinatoire relativement simple et une structure additionnelle, permettant souvent de déterminer f.

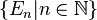
Certaines fonctions de comptage, sont données par des formules « fermées », et peuvent être exprimées comme composées de fonctions élémentaires telles que des factorielles, des puissances, et ainsi de suite.

Cette approche peut ne pas être entièrement satisfaisante (ou pratique) pour certains problèmes combinatoires. Par exemple, soit f(n) le nombre de sous-ensembles distincts de nombres entiers dans l'intervalle [1, n] qui ne contiennent pas deux nombres entiers consécutifs. Par exemple, avec n = 4, nous obtenons ∅, { 1 }, { 2 }, { 3 }, { 4 }, { 1, 3 }, { 1, 4 }, { 2, 4 }, et donc f(4) = 8. Il s'avère que f(n) est le nème nombre de Fibonacci, qui peut être exprimé sous la forme « fermée » suivante :

où φ = (1 + √5)/2, est le nombre d'or. Cependant, étant donné que nous considérons des ensembles de nombres entiers, la présence du √5 dans le résultat peut être considérée comme inesthétique d'un point de vue combinatoire. Aussi f(n) peut-il être exprimé par une relation de récurrence :

f(n) = f(n - 1) + f (n - 2)

ce qui peut être plus satisfaisant (d'un point de vue purement combinatoire), puisque la relation montre plus clairement comment le résultat a été trouvé.

Dans certains cas, un équivalent asymptotique g de f,

f(n)~g(n) quand n tend vers l'infini

où g est une fonction « familière », permet d'obtenir une bonne approximation de f. Une fonction asymptotique simple peut être préférable à une formule « fermée » extrêmement compliquée et qui informe peu sur le comportement du nombre d'objets. Dans l'exemple ci-dessus, un équivalent asymptotique serait :

quand n devient grand.

Une autre approche est celle des séries entières. f(n) peut être exprimé par une série entière formelle, appelée fonction génératrice de f, qui peut être le plus couramment :

• la fonction génératrice ordinaire

• ou la fonction génératrice exponentielle

Une fois déterminée, la fonction génératrice peut permettre d'obtenir toutes les informations fournies par les approches précédentes. En outre, les diverses opérations usuelles comme l'addition, la multiplication, la dérivation, etc., ont une signification combinatoire ; et ceci permet de prolonger des résultats d'un problème combinatoire afin de résoudre d'autres problèmes.