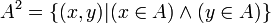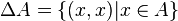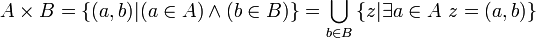Produit cartésien - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
- Cet article fait référence au concept mathématique sur les ensembles. Pour les graphes, voir produit cartésien de graphes.
En mathématiques, le produit cartésien de deux ensembles X et Y, appelé ensemble-produit, est l'ensemble de tous les couples, dont la première composante appartient à X et la seconde à Y. On généralise facilement la notion de produit cartésien binaire à celle de produit cartésien fini, qui est alors un ensemble de multiplets, on dit n-uplets pour les éléments d'un produit cartésien de n ensembles. On peut aussi introduire la notion de somme disjointe (ou cartésienne). Pour généraliser aux produits cartésiens infinis, des produits d'une famille quelconque (éventuellement infinie) d'ensembles, on a besoin de la notion de fonction.
Les produits cartésiens doivent leur nom à René Descartes, qui, en créant la géométrie analytique, a le premier utilisé ce que nous appelons maintenant,
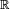
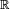
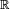
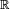
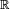
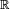
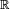
Produit cartésien de deux ensembles
Définition
Pour tout ensemble A et tout ensemble B, il existe un unique ensemble dont les éléments sont les couples dont la première composante appartient à A et la seconde à B :
Cet ensemble est noté « A x B » (lire « A croix B ») et il est appelé produit cartésien de A par B.
Si on considère couples et produits cartésiens comme une notion primitive, on aura comme axiome cette propriété d'existence et d'unicité. Elle se démontre en théorie des ensembles, pour la représentation des couples choisie.
Exemple
Si A est l'ensemble { A, R, D, V, 10, 9, 8, 7, 6, 5, 4, 3, 2 } et B l'ensemble { pique, cœur, carreau, trèfle }, alors le produit cartésien de ces deux ensembles est un jeu classique de 52 cartes, soit l'ensemble suivant :
- { (A, pique) ... (2, pique) , (A, cœur) ... (2, coeur) , (A, carreau) ... (2, carreau) , (A, trèfle) ... (2, trèfle) }.
Propriétés
- On déduit directement de la définition que le produit cartésien d'un ensemble par l'ensemble vide est égal à l'ensemble vide, c'est-à-dire que pour tout ensemble A :
- Si A et B sont de cardinaux finis, alors le cardinal de A x B est égal au produit des cardinaux de A et de B.
- En règle générale, B x A ≠ A x B. Plus précisément, pour deux ensembles quelconques A et B :
- A x A est noté A2 (lire « A au carré ») et appelé carré cartésien de A :
A2 ne doit pas être confondu avec ΔA (lire « delta A »), diagonale de A :
Remarque : La diagonale d'un ensemble se confond avec son carré cartésien si et seulement si cet ensemble est vide ou se réduit à un singleton.
- Les sous-ensembles d'un produit cartésien sont appelés graphes.
Représentation en théorie des ensembles
En théorie des ensembles, si on choisit, comme usuellement, la représentation des couples de Kuratowski, les couples dont la première composante est dans A et la seconde dans B sont des éléments de
![\ P[P(A\cup B)]](https://static.techno-science.net/illustration/Definitions/autres/d/d1079ab72d05dea35a06ac9c0ab92277_e6e692c374c4373a6714a489089676dc.png)
On peut donc définir le produit cartésien par compréhension, on aura bien sûr besoin des couples, donc, en plus des axiomes précédents, de l'axiome de la paire et du schéma d'axiomes de compréhension :
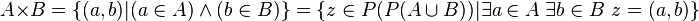
On peut aussi définir le produit cartésien en utilisant le schéma d'axiomes de remplacement au lieu de l'ensemble des parties :
Représentation en théorie des catégories
Dans la catégorie des ensembles, étant donnés deux objets S et T il existe un objet P et deux morphismes
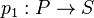
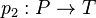
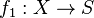
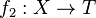
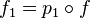
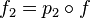
Dans une catégorie quelconque, un produit P n'existe pas toujours, et quand il existe, il sera unique à isomorphisme unique près. En particulier, toutes les structures ainsi obtenues sont isomorphes, ce qui permet de définir le produit cartésien SxT.
![\forall A \; \forall B \; \exists! P\;\forall x \; \forall y \;[( x \in A \wedge y \in B ) \Leftrightarrow ( x , y ) \in P]](https://static.techno-science.net/illustration/Definitions/autres/a/a7483b1789c4bfb820be5395c01c7d72_b389f4af23d825a40c99a0c7799246e4.png)
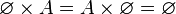
![[A \times B \ne B \times A] \Leftrightarrow [( A \ne B ) \wedge ( A \ne \varnothing ) \wedge ( B \ne \varnothing )]](https://static.techno-science.net/illustration/Definitions/autres/3/3815207e3f1188c8852ff19104122441_cc471f3269bcd6acd9d8aa80e43bd45f.png)