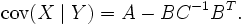Complément de Schur - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Applications aux probabilités et à la statistique
Soit (X,Y) un vecteur gaussien de Rn+m de matrice de covariance
![V=\operatorname{cov}(X,Y)=\left[\begin{matrix} A & B \\ B^T & C \end{matrix}\right].](https://static.techno-science.net/illustrationWebp/Definitions/autres/e/eccca9e6360388294ec6cc63539a925f_71833092c8c961db3db22e8f43eea305.png)
Ici, X (respectivement Y) est un vecteur gaussien de Rn (respectivement Rm) de matrice de covariance A (respectivement C).
La loi conditionnelle de X sachant Y est encore une loi gaussienne multivariée de dimension n. Supposons que la matrice V est inversible (elle est donc symétrique et définie positive). Alors, la matrice de covariance de la loi conditionnelle de X sachant Y ne dépend pas de Y et est donnée par le complément de Schur de C dans V.
Cela montre en particulier que le complément de Schur d'un bloc diagonal d'une matrice de covariance empirique d'un échantillon gaussien suit une loi de Wishart (tout comme la matrice de covariance empirique elle-même).
