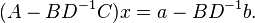Complément de Schur - Définition

Introduction

En algèbre linéaire et plus précisément en théorie des matrices, le complément de Schur est défini comme suit. Soit

une matrice de dimension (p+q)×(p+q), où les blocs A, B, C, D sont des matrices de dimensions respectives p×p, p×q, q×p and q×q, avec D inversible. Alors, le complément de Schur du bloc D de la matrice M est constitué par la matrice de dimension p×p suivante :

A − BD ^{− 1}C.

Lorsque B est la transposée de C, la matrice M est symétrique définie-positive si et seulement si D et son complément de Schur dans M le sont.

Le complément de Schur apparaît en particulier comme le résultat d'une élimination de Gauss «partielle» en multipliant la matrice M à droite avec la matrice «triangulaire inférieure» par blocs suivante

Ici, I_p désigne la matrice identité de dimension p×p. Après multiplication par la matrice LT, le complément de Schur apparaît dans le bloc p×p supérieur. La matrice produit est

L'inverse de M peut ainsi être exprimée en termes de D ^{− 1} et de l'inverse du complément de Schur

ou encore plus simplement,

Application à la résolution d'équations linéaires

Le complément de Schur apparaît naturellement lors de la résolution d'un système d'équations linéaires de la forme

Ax + By = a

Cx + Dy = b

où

• x et a sont des vecteurs colonne de dimension p,
• y et b sont des vecteurs colonne de dimension q,
• A, B, C, D sont comme précédemment.

En multipliant la seconde équation par BD ^{− 1} puis en la soustrayant de la première, il vient

Ainsi, la résolution de cette équation en x est possible dès que D et son complément de Schur sont inversibles. Il est ensuite possible d'obtenir y en résolvant l'équation Cx + Dy = b. Cette méthode réduit le problème de l'inversion d'une matrice de dimension à celui de l'inversion de deux matrices de dimensions respectives p×p et q×q. En pratique, la matrice D doit être bien conditionnée pour rendre la méthode précise.

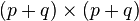
Bibliographie

• Chapitre 7 du livre de R. A. Horn et C. R. Johnson, intitulé « Matrix Analysis », plusieurs fois édité par Cambridge University Press.

v · d · m Algèbre linéaire générale
Vecteur • Scalaire • Combinaison linéaire • Espace vectoriel • Matrice
Famille de vecteurs	Famille génératrice • Famille libre (indépendance linéaire) • Base • Théorème de la base incomplète • Rang • Colinéarité
Sous-espace	Sous-espace vectoriel • Somme d'ensembles • Somme directe • Sous-espace supplémentaire • Dimension • Codimension • Droite • Plan • Hyperplan
Morphisme et notions relatives	Application linéaire • Noyau • Conoyau • Lemme des noyaux • Pseudo-inverse • Théorème de factorisation • Théorème du rang • Équation linéaire • Système d'équations linéaires • Élimination de Gauss-Jordan • Forme linéaire • Espace dual • Orthogonalité • Base duale • Endomorphisme linéaire • Valeur propre, vecteur propre et espace propre • Spectre • Projecteur • Symétrie • Matrice diagonalisable • Diagonalisation • Endomorphisme nilpotent
En dimension finie	Espace vectoriel de dimension finie • Trace • Déterminant • Polynôme caractéristique • Polynôme d'endomorphisme • Théorème de Cayley-Hamilton • Polynôme minimal d'un endomorphisme • Invariants de similitude • Réduction d'endomorphisme • Réduction de Jordan • Décomposition de Dunford • Décomposition de Frobenius
Enrichissements de structure	Norme • Produit scalaire • Forme quadratique • Espace vectoriel topologique • Orientation • Algèbre sur un corps • Algèbre de Lie • Complexe différentiel
Développements	Théorie des matrices • Représentation de groupe • Analyse fonctionnelle • Algèbre multilinéaire • Module sur un anneau