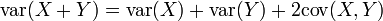Covariance - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En statistiques, la covariance est un nombre permettant d'évaluer le sens de variation de deux variables et, ainsi, de qualifier l'indépendance de ces variables.
Si deux variables sont indépendantes, leur covariance est nulle, mais la réciproque n'est pas toujours vraie.
Définition
En théorie des probabilités et en statistique, on nomme covariance de deux variables aléatoires réelles X et Y la valeur :
Définition —
![\operatorname{cov}(X,Y)\equiv E[(X-E[X])\,(Y-E[Y])]](https://static.techno-science.net/illustration/Definitions/autres/4/43950512170ec68b9a165a54ddab2aeb_46284bda3873afde40371af5d5132366.png)
-
- où E désigne l'espérance mathématique.
Notation — On note parfois
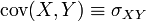
Intuitivement, la covariance est une mesure de la variation simultanée de deux variables aléatoires. C'est-à-dire que la covariance devient plus positive pour chaque couple de valeurs qui diffèrent de leur moyenne dans le même sens, et plus négative pour chaque couple de valeurs qui diffèrent de leur moyenne dans le sens opposé.
L'unité de mesure de la covariance cov(X,Y) est le produit de l'unité des variables aléatoires X et Y et sa valeur est comprise dans
![]-\infty; +\infty[](https://static.techno-science.net/illustration/Definitions/autres/0/0b56a082ba29d81bd37f0d5f372190aa_453eb713cae6cf3faeef345d695dd91d.png)
Dans le cas de variables discrètes, on a:
-
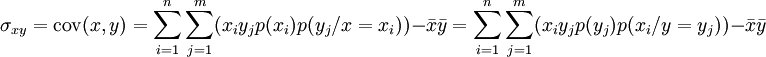
- tandis que:
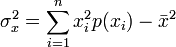
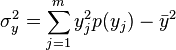
- tandis que:
Exemple
Dans un forum Internet, quelqu'un affirme que l'activité du forum est plus intense les jours de pleine lune. On peut ne pas disposer du calendrier des pleines lunes, mais si cette affirmation est exacte et si l'on nomme N(t) le nombre de contributions au jour t, la covariance entre N(t) et N(t+28) cumulée sur toutes les valeurs de t sera probablement supérieure aux covariances entre N(t) et N(t+x) pour les valeurs de x différentes de 28.
Propriétés
Par analogie avec le théorème de König-Huyghens pour la variance, on a:
Propriété —
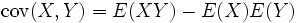
La seconde propriété est utile pour les cas de variables X et Y indépendantes
Propriété — X et Y indépendantes
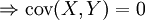
Propriété — X et Y indépendantes
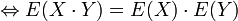
-
- La réciproque, cependant, n'est pas vraie. Il est en effet possible que X et Y ne soient pas indépendantes, et que leur covariance soit nulle. Des variables aléatoires dont la covariance est nulle sont dites non corrélées.
Propriété —
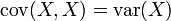
Propriété —
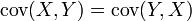
Propriété —
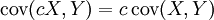
Propriété —
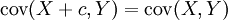
Bilinéarité de la covariance:
Propriété —
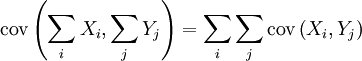
-
- Ceci traduit le fait que la covariance est une forme bilinéaire symétrique positive (sur l'espace vectoriel
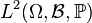
- Ceci traduit le fait que la covariance est une forme bilinéaire symétrique positive (sur l'espace vectoriel
-
- Cette formule est l'analogue de (x + y)2 = x2 + y2 + 2xy . En fait, la plupart des propriétés de la covariance sont analogues à celles du produit de deux réels ou du produit scalaire de deux vecteurs.
Propriété —
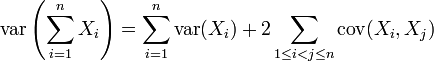
-
- Cette formule est classique pour une forme quadratique associée à une forme bilinéaire symétrique.
![\operatorname{cov}(X,Y)\equiv E[(X-E[X])\,(Y-E[Y])]=E(X Y) - E(X)E(Y)=E(X)E(Y)-E(X)E(Y)=0](https://static.techno-science.net/illustration/Definitions/autres/f/f95750e193fd32347fc915cba1c45a1e_ebc5c393dbd53188f34359ba5e80a99d.png)