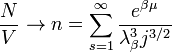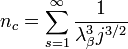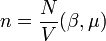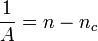Condensation de Bose-Einstein généralisée - Définition

Formulation mathématique du concept

Critère de condensation usuel à la Einstein et London

Nous donnons ici la formulation mathématique du concept de condensation de Bose-Einstein original tel qu'il fut formulé par Einstein en premier lieu. On se place dans l'ensemble grand-canonique (volume constant V, température T, potentiel chimique μ), dans le cas du gaz parfait de boson dans une boîte cubique , on a condensation de Bose-Einstein si on a occupation macroscopique de l'état fondamental en limite de volume infini (densité de particule sans vitesse strictement positive):

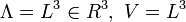
Il explique cela par le fait que la partie excité du gaz a une densité:

qui sature à une valeur constante (pour le potentiel chimique nul):

où β = 1 / k_BT (avec k_B la constante de Boltzmann) et la longueur d'onde thermique de de Broglie.

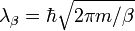
Cette formulation a été reprise par Fritz London en 1938 de manière plus explicite et plus précise de sorte à mettre terme à la controverse présentée par Ulhenbech dans sa thèse de 1927 critiquant la validité mathématique de l'hypothèse d'Einstein. London dit que pour une densité fixée n = N / V, le potentiel chimique μ devient une solution de l'équation:

ainsi pour chaque valeur du volume V, μ prend une certaine valeur qui dépend de β, de la densité n et du volume V. En choisissant μ = − A / βV + O(1 / V) comme asymptotique de la solution on obtient que la densité de particule dans l'état fondamentale s'écrit:

A est alors solution de l'équation:

Condensation généralisée à la van den Berg-Lewis-Pulé

Classification de la condensation généralisée

Critère de condensation pour l'état fondamental