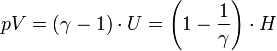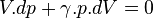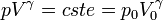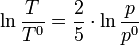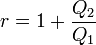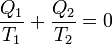Gaz parfait - Définition

Introduction

Le gaz parfait est un modèle thermodynamique décrivant le comportement de tous les gaz réels à basse pression.

Ce modèle a été développé au XIX^e siècle en constatant que tous les gaz tendent vers ce même comportement à pression suffisamment basse, quelle que soit la nature chimique du gaz ce qu'exprime la loi d'Avogadro, découverte en 1811 : la relation entre la pression, le volume et la température est, dans ces conditions, indépendante de la nature du gaz. Cette propriété s'explique par le fait que lorsque la pression est faible, les molécules de gaz sont suffisamment éloignées les unes des autres pour pouvoir négliger les interactions d'ordre électrostatique qui dépendent, elles, de la nature physico-chimique du gaz (molécules plus ou moins polaires). De nombreux gaz réels vérifient avec une excellente approximation le modèle du gaz parfait, dans les conditions normales. C'est le cas des gaz principaux de l'air, le diazote et le dioxygène.

Description d'un gaz parfait

Sur les plans macroscopiques, on appelle gaz parfait tout gaz vérifiant simultanément :

loi de Boyle-Mariotte 

à température constante, le produit de la pression p par le volume V : pV est considéré comme constant lorsque la pression est faible ;

loi d'Avogadro 

tous les gaz ont le même volume molaire dans les mêmes conditions de pression et de température.

Sur le plan microscopique, la théorie cinétique des gaz permet de retrouver ce comportement de gaz parfait : un gaz parfait est un gaz dont les molécules n'interagissent pas entre elles en dehors des chocs et dont la taille est négligeable par rapport à la distance intermoléculaire moyenne. L'énergie du gaz parfait est donc la somme de l'énergie cinétique du centre de masse des molécules et de l'énergie interne de chaque molécule (rotation, oscillation). Lorsque ces deux énergies sont proportionnelles, on a le .

Gaz parfait de Laplace

Définition

Il arrive que ne dépende pas de , donc n'en dépend pas non plus. Le gaz parfait est dit de Laplace (le GP de Laplace). Il arrive souvent que l'on précise la valeur de .

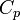
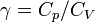
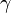
Par convention, si on choisit γ = 5 / 3, le gaz parfait de Laplace est dit « gaz parfait monoatomique » (GPM). Le comportement de l'argon est très proche d'un gaz parfait monoatomique.

Par convention, si on choisit γ = 7 / 5 le gaz parfait de Laplace est dit « gaz parfait diatomique » (GPD). Le comportement du diazote N₂ est proche d'un gaz parfait diatomique.

Il est d'usage d'écrire pour un gaz parfait de Laplace :

soit, pour un gaz parfait monoatomique

pV = 2/3 U = 2/5 H

et pour un gaz parfait diatomique :

pV = 2/5 U = 2/7 H.

Loi de Laplace

Dans une transformation adiabatique réversible élémentaire, . Ceci entraîne, en remplaçant U par sa valeur en fonction de p et V :

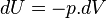
Soit en intégrant, la Loi de Laplace :

d'où le nom donné à ces gaz parfaits.

Il en résulte, dans une détente, un refroidissement considérable, le gaz prenant sur son énergie interne le travail, (-W ), qu'il fournit.

Application numérique

Pour un gaz parfait monoatomique, on trouve aisément :

Soit pour un rapport de pression 1/10 (la pression baisse de 90 %), un abaissement de température absolue d'un facteur 0,398 ; de 300 K la température descend à 120 K soit une chute de 180 K. Ce procédé est utilisé dans l'industrie pour obtenir de basses températures. Malheureusement, la valeur obtenue ne réflète pas réalité, car les gaz réels ne sont pas des gaz parfaits à basse température.

Pour les ordres de grandeur, on retient R·T ~ 2 500 J/mol à 300 K. Le travail récupéré dans cette détente est 2500·(180/300) = 900 J/mol.

Expérience : détente dans un récipient vide

Une autre loi remarquable est l'échauffement produit quand on laisse pénétrer un gaz parfait de Laplace dans un flacon vide. Le gaz s'engouffre et puis très vite tout redevient chaotique : la température s'uniformise et devient

T = γT₀

T₀ étant la température externe. Pour une température externe de 300 K et un gaz parfait monoatomique, on obtient :

T = 500 K

soit une élévation de 200 K. Dans la soufflerie de Modane, c'est bien ce que l'on peut observer.

Ainsi, on a deux cas d'expansion du gaz.

Cycle de Carnot d'un gaz parfait de Laplace

Un cycle de Carnot moteur d'un gaz parfait a comme le veut le théorème de Carnot, le rendement de Carnot :

.

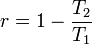
Dans le cas présent, tout peut se calculer aisément. Décrivons le cycle — on pourra le dessiner aisément en coordonnées de Clapeyron logarithmiques (log V, log p) :

1. Transformation (A → B) : compression isotherme à température basse, T₂, réversible : il faut donc, pour éviter que le gaz ne s'échauffe, libérer une quantité de chaleur -Q₂ >0 à la source froide qui maintient la température T₂.
2. Transformation (B → C) : compression de Laplace : la température monte de T₂ à T₁.
3. Transformation (C → D) : détente isotherme à haute température T₁, réversible : pour éviter que le gaz ne se refroidisse, il faut que la source chaude fournisse une quantité de chaleur Q₁>0.
4. Transformation(C → A) (le point C a été choisi à l'intersection de l'adiabatique réversible passant par A) : la détente adiabatique réversible ramène la température de T₁ à T₂, et le gaz à son état initial.

Fin du cycle.

Puisque le gaz est revenu à son état initial, le premier principe de la thermodynamique nous dit que

W + Q₁ + Q₂ = 0

Le rendement du moteur est le travail récupéré -W (donc égal à Q₁ + Q₂) divisé par la quantité de chaleur délivrée par la source chaude, soit Q₁ :

On démontre que

d'où

.

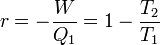
Ce qui nous donne la formule annoncée.

L'égalité de Clausius

provient du fait que le cycle a été réversible : l'entropie totale est restée constante, celle du gaz est nulle car il est revenu dans l'état A. La source 1 a vu son entropie varier de -Q₁/T₁, la source 2 de -Q₂/T₂, d'où l'égalité.

Application numérique : même en prenant une eau de rivière à 300 K et une source chaude à 600 K, le rendement ne serait que 50 %. Sur un gigawatt électrique fourni par une centrale « reversible », 2GW doivent être consommés (en charbon, pétrole, méthane, ou mox nucléaire) dont 1 GW ira à la rivière (élévation de température) ou dans l'atmosphère (chaleur de fumée, vapeur d'une tour de réfrigération). Si l'on considère que toute la chaleur va dans la rivière et que celle-ci a un débit 100 m³/s : en 1 seconde, 10⁹ J iront chauffer 100×10⁶ g d'eau : soit une élévation de température de 10 (J)/4,18 (J/K) = 2,4 K.

Six centrales produisant 6 GW donneraient une élévation de 6·2,4 = 14,4 K. En France, il est interdit de dépasser 27 °C dans une rivière (obligation légale, pour la survie de la vie aquatique en zone tempérée) : l'été 2003 fut très chaud, il a fallu arrêter certaines centrales (voir l'article Canicule 2003). Cette pollution thermique (Q₂ < 0) calculée par la formule de Carnot est la plus basse possible ; il s'agit en fait d'un minimum, la pollution thermique réelle est plus élevée. Encore avons-nous pris un rendement r = 0,5 ; la réalité est proche de 0,42.