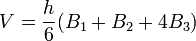Volume - Définition

Introduction

Le volume, en sciences physiques ou mathématiques, est une grandeur qui mesure l'extension d'un objet ou d'une partie de l'espace.

• En physique, le volume d'un objet mesure « l'extension dans l'espace » qu'il possède dans les trois directions en même temps, de même que l'aire d'une figure dans le plan mesure « l'extension » qu'elle possède dans les deux directions en même temps.

• En mathématiques, le volume d'une partie de l'espace est sa mesure au sens de la théorie de la mesure de Lebesgue.

Mesure du volume

• Le volume physique se mesure en mètre cube dans le système international. On utilise fréquemment le litre, notamment pour des liquides et pour des matières sèches. Ainsi, on considère le volume comme une grandeur extensive et la grandeur intensive thermodynamique associée est la pression.

• En mathématique, et plus précisément en géométrie euclidienne, le volume du parallélépipède engendré par 3 vecteurs non coplanaires se calcule grâce au produit mixte des trois vecteurs :

.

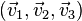
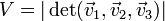
Les calculs de volume ont évolué au cours de l'histoire en suivant les progrès du calcul infinitésimal. C'est ainsi que les premiers volumes ont été calculés grâce à la méthode d'exhaustion, puis en utilisant le principe de Cavalieri et pour finir en calculant des intégrales triples.

Pour les solides simples (parallélépipède et objets de révolution), il existe des formules mathématiques permettant de déterminer leur volume d'après leurs dimensions caractéristiques.

Quelques formules

Dans la suite on notera

• V le volume
• B et b les aires de la grande base et de la petite base
• H la hauteur (ou distance séparant les deux faces)
• D ou d le diamètre
• R ou r le rayon
• a l'arête
• L ou l la longueur et la largeur d'un rectangle

Les solides de Platon

Ce sont les cinq seuls polyèdres réguliers. Si l'arête du polyèdre est a, on a

• Pour le tétraèdre :
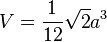
• Pour le cube :
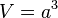
• Pour l'octaèdre :
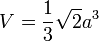
• Pour le dodécaèdre :
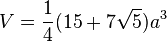
• Pour l'icosaèdre : où est le nombre d'or

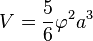
Les prismes et cylindres

La formule générale est toujours : Aire de la base × Hauteur

• Le prisme droit :
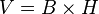
• Le parallélépipède rectangle ou pavé :
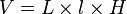
• Le cylindre de révolution :

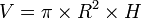
Les pyramides et cônes

La formule générale est toujours :

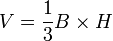
• Le cône de révolution :
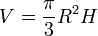
• La pyramide tronquée par un plan parallèle à la base :

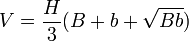
La boule

• La boule a pour volume ou
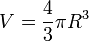
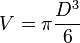
• Pour une calotte sphérique, où R est le rayon de la boule et H la hauteur de la calotte.
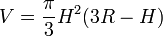
• Le volume de la boule percée d'un cylindre (rond de serviette) ne dépend pas du rayon de la boule :
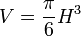
• Le secteur sphérique (intersection entre un cône de sommet O et la boule de centre O : où H est la hauteur de la calotte et R le rayon de la boule.

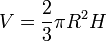
Solides de révolution

Le théorème de Guldin (ou règle de Pappus) permet de calculer le volume d'un solide de révolution engendré par la révolution d'un élément de surface S plane autour d'un axe situé dans son plan et ne le coupant pas, pour peu que l'on connaisse le centre de gravité G de l'élément de surface S.

où R est la distance séparant le point G de l'axe de rotation.

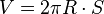
Cette formule permet de déterminer les volumes suivants :

• le tore : V = 2π²Rr² où r est le rayon du cercle de centre G tournant autour de l'axe (Δ) et où R est la distance de G à (Δ).
• le tonneau : Kepler donne une formule approchée pour le volume d'un tonneau, qui se révèle exacte lorsque le tonneau est engendré par une sphère, une pyramide, un hyperboloïde à une nappe, un paraboloïde elliptique, un ellipsoïde de révolution. Si B₁ et B₂ sont les surfaces des bases et B₃ la surface de la section à mi-hauteur alors

Autres

• Le conoïde circulaire droit (exemple l'incisive) : où R est le rayon du cercle de base et H la hauteur du conoïde.
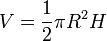
• Le lingot (hexaèdre formé de deux bases rectangulaires parallèles et de 4 faces latérales trapézoïdales) . On retrouve la formule de Kepler : où B₁ et B₂ sont les surfaces des deux bases rectangulaires et B₃ la surface de la section à mi-hauteur. Cette formule est très employée en génie civil dans les calculs de volume et plus particulièrement pour les mouvements de terres dans le domaine des travaux publics où elle est connue sous le nom de formule du tas de cailloux ou encore formule du tas de sable.