Ensemble grand-canonique - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En physique statistique, l’ensemble grand-canonique est un ensemble statistique, dans lequel chaque système est en équilibre avec un réservoir externe d'énergie et de particules. Cela signifie que le système peut échanger de l’énergie et des particules avec le réservoir, autrement dit, l’énergie et le nombre de particules sont alors amenés à fluctuer d’un système à un autre de l’ensemble.
Cet ensemble est utilisé lorsque le nombre de particules ne peut pas être fixé, plus particulièrement pour les systèmes composés de bosons et de fermions.
Introduction
Dans cet ensemble, on considère que le système est composé de particules identiques, et on introduit le potentiel chimique, pour prendre en considération la variation du nombre de particules. Le réservoir doit être considéré grand devant le système, afin que les échange d’énergie et de particules n’influent pas sur la température du réservoir, et donc sur la température du système. Le réservoir doit alors se comporter comme un thermostat et imposer sa température au système.
On considère l’hamiltonien du système défini comme :
où
Pour chaque ensemble miscrocopique
Suivant que le système considéré est composé de bosons, ou de fermions, ni est soumis aux conditions suivantes :
Observable miscrocopique
Fonction de partition
La fonction de partition est définie comme étant :
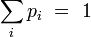
![\Xi = \sum_{\{|n_i\rangle\} } e^{ -\beta \big[ E \left(|n\rangle\right) - \mu N\left(|n\rangle\right)\big] } = \sum_{ \{ |n_i \rangle \} } e^{ -\beta \sum_i \left(E_i - \mu \right)n_i }](https://static.techno-science.net/illustrationWebp/Definitions/autres/0/01bde60818ad303fc1e197dbd21b7f29_63ad262c484cf8eb0c13223856ea29f5.png)
où
On peut écrire Ξ comme :
avec
Probabilité d'un micro-état
La probabilité pour que le système soit dans un micro-état i est défini par :
où
