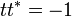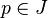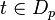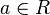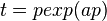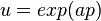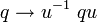Coquaternion - Définition

Application à la cinématique

En utilisant les bases données ci-dessus, on peut montrer que l'application

est une rotation ordinaire ou hyperbolique suivant que

, ou , .

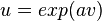
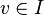
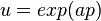
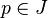
Ces applications sont des projections dans la géométrie d'anneau inversible des coquaternions. La collection de ces applications produit une certaine relation avec le groupe de Lorentz puisque il est aussi composé des rotations ordinaires et hyperboliques. Parmi les particularités de cette approche par rapport à la cinématique relativiste, on trouve le profil anisotropique, comparé aux quaternions hyperboliques.

Le frein à l'usage des coquaternions pour les modèles cinématiques peut s'expliquer par la signature de l'espace-temps (2, 2) qui est présumé avoir comme signature (1, 3) ou (3, 1). Néanmoins, une cinématique relativiste plus claire apparait lorsqu'un point de la contre-sphère est utilisé pour représenter un cadre d'inertie de référence. Si , alors, il existe un tel que , et un tel que . Alors, si et , l'ensemble est une base orthogonale issue de t, l'orthogonalité se poursuit à travers les applications des rotations ordinaires ou hyperboliques.