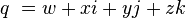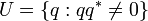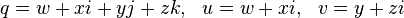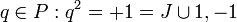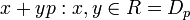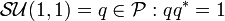Coquaternion - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques et en algèbre abstraite, un coquaternion est une idée mise en avant par James Cockle en 1849. Comme les quaternions de Hamilton découverts en 1843, ils forment un espace vectoriel réel à quatre dimensions muni d'une opération multiplicative. À la différence de l'algèbre des quaternions, les coquaternions peuvent avoir des diviseurs de zéro, des éléments idempotents ou nilpotents.
L'ensemble
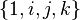
-
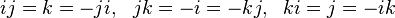
-
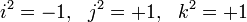
Avec ces produits l'ensemble
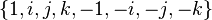
Un coquaternion
possède un conjugué
-
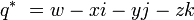
-
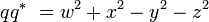
Lorsque le module est différent de zéro, alors q possède un inverse multiplicatif.
est l'ensemble des unités. L'ensemble P de tous les coquaternions forme un anneau
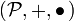
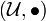
Soit
où u et v sont des nombres complexes ordinaires. Alors la matrice complexe
-
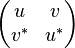
où
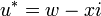
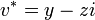
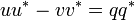
Profil
Soit
-
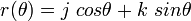
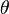
-
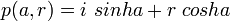
-
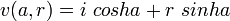
-
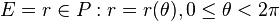
-
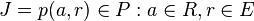
-
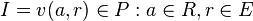
Maintenant, il est facile de vérifier que
et que
-
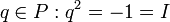
Ces égalités d'ensembles signifient que lorsque
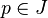
est un sous-anneau de P, c’est-à-dire isomorphe au plan des nombres complexes fendus lorsque v est dans I alors
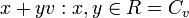
est un sous-anneau planaire de P qui est isomorphe au plan complexe ordinaire C.
Pour chaque
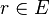
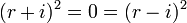
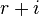
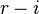
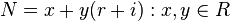
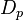
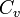
est formée des "cercles unités" dans les plans constitués de P. Dans
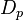
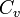
Géométrie de la contre-sphère
Prenons
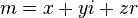
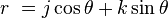
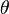
-
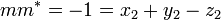
Puisque les points sur la contre-sphère doivent se trouver sur un contre-cercle dans un certain plan
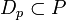
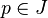
-
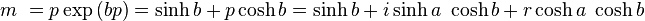
Soit
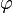
-
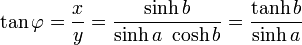
Comme b peut devenir grand, tanh b est proche de un. Alors
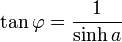
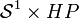
Orthogonalité plane
Lorsque le coquaternion
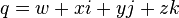
Définition : pour les coquaternions différents de zéro q et t, nous écrivons
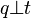
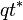
- Pour chaque
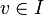
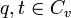
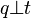
- Pour chaque
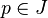
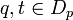
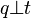
- Pour chaque
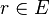
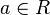
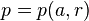
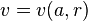
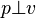
- Si u est une unité dans l'anneau des coquaternions, alors
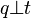
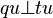
-
- Preuve :
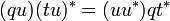
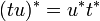
- Preuve :