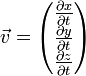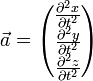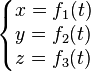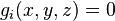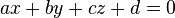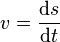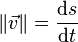Cinématique - Définition

Introduction

En physique, la cinématique est la discipline de la mécanique qui étudie le mouvement des corps, en faisant abstraction des causes du mouvement (celles-ci sont généralement modélisées par des forces et des moments). Elle utilise la géométrie analytique.

On peut dater la naissance de la cinématique moderne à l'allocution de Pierre Varignon le 20 janvier 1700 devant l'académie royale des sciences de Paris. À cette occasion il définit la notion d'accélération et montre comment il est possible de la déduire de la vitesse instantanée à l'aide d'une simple procédure de calcul différentiel.

Définitions de base

Il faut d'abord définir un référentiel, c'est-à-dire un repère de l’espace et une référence pour le temps, une horloge ; on utilise en général le référentiel lié au laboratoire, par exemple dont les axes suivent les arêtes des murs de la pièce, ou bien celle de la table, ou encore les directions géographiques Nord-Sud, Est-Ouest et haut-bas (si le laboratoire est immobile par rapport au sol). L'objet de base est le point, dont les dimensions nulles, et qui est défini par ses coordonnées M(x,y,z,t).

Concrètement, cet objet physique défini par quatre paramètres représente soit un objet de petite taille (particule, petite bille), soit un objet de grande taille dont on néglige les effets de rotation sur lui-même ; nous appellerons cet objet le mobile. On ne s’intéresse alors qu'au mouvement dans l'espace du centre d’inertie de ce mobile. Le centre d’inertie d'un objet est encore appelé centre de masse ou centre de gravité.

Les coordonnées définissent le vecteur-position, qui dépend ainsi de la position et du temps.

Le vecteur obtenu en dérivant les coordonnées par rapport au temps définit le vecteur-vitesse. Le vecteur vitesse est indépendant du choix du point origine.

Le vecteur obtenu en dérivant les composantes du vecteur vitesse par rapport au temps définit le vecteur-accélération

La mécanique du point permet de prévoir la position en fonction du temps, à partir de la vitesse initiale et des forces.

L'équation horaire du mouvement

correspond à l’équation paramétrique d'une courbe ; on peut souvent réduire ceci à un système d’équations cartésiennes

qui, dans le cas le plus simple, sont du type linéaire

Cette courbe est l’ensemble des points par où passe le centre d'inertie du mobile. On définit alors l’abscisse curviligne, notée s, la distance parcourue sur la courbe par rapport à un point de référence (la position du centre d'inertie du mobile à t = 0). Pour un petit déplacement de M(x, y, z) à M'(x + dx, y + dy, z + dz), l'abscisse curviligne est assimilable à un segment, d'où :

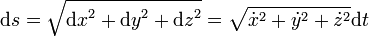
On a donc .

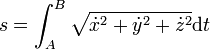
La notion commune de vitesse est en fait la dérivée de l'abscisse curviligne. On parle souvent de vitesse scalaire :

On a en fait

Définition de l'abscisse curviligne

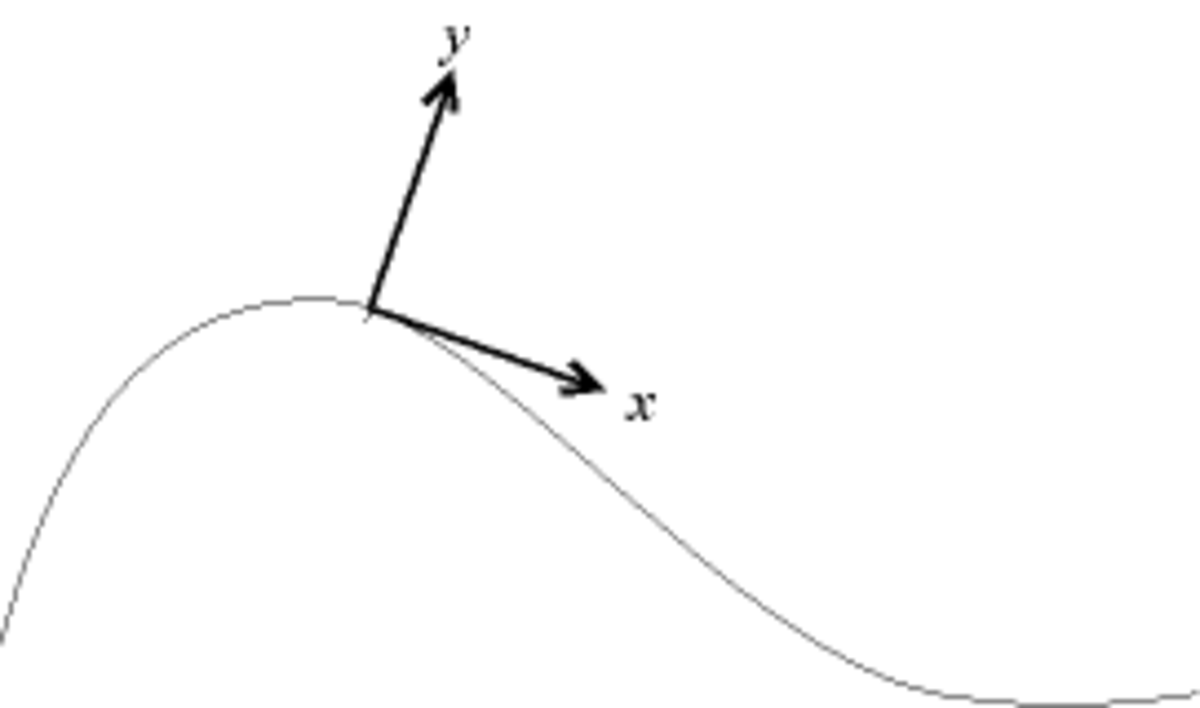
On ne considère en général, pour simplifier l'étude, que des mouvements plans (que le plan soit horizontal, vertical ou incliné). On définit donc un repère dans ce plan, ce qui permet de ne travailler qu'avec deux coordonnées.

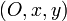
Pour simplifier les calculs, on définit souvent un repère local dit « de Frenet » pour chaque instant ; en un point de la courbe, l'axe des est la tangente à la courbe et orienté dans le sens du mouvement, et l'axe des y est la normale à la courbe orienté de sorte que le repère soit direct. Ce n'est pas un référentiel mobile par rapport au référentiel de l'étude, c'est un repère « jetable », défini juste à un instant t pour simplifier l'écriture des grandeurs à cet instant donné. Le référentiel reste celui du laboratoire, seule change la manière dont on exprime les composantes des vecteurs.

Définition du repère de Frenet