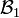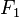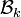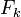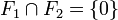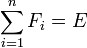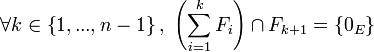Somme directe - Définition

Introduction

En mathématiques, et plus précisément en algèbre, le terme de somme directe désigne des ensembles munis de certaines structures, construits à partir de la réunion d'autres ensembles du même type.

Somme directe de sous-espaces vectoriels

Somme directe de deux sous-espaces vectoriels

Soient F₁ et F₂ deux sous-espaces vectoriels de l’espace vectoriel E. On dit que F₁ et F₂ sont en somme directe si et seulement si pour tout élément u de F₁ + F₂, il existe un unique couple de tel que u = u₁ + u₂.

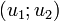
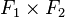
On dit aussi dans ce cas que la somme F₁ + F₂ est directe.

En d'autres termes, la somme de deux sous-espaces vectoriels F₁ et F₂ est directe si la décomposition de tout élément de F₁ + F₂ en somme d'un élément de F₁ et d'un élément de F₂ est unique.

La somme sera alors notée : .

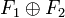
On dispose des caractérisations usuelles suivantes :

• F₁ et F₂ sont en somme directe si et seulement si, pour tout u₁ de F₁ et u₂ de F₂,

• F₁ et F₂ sont en somme directe si et seulement si

• F₁ et F₂ sont en somme directe si et seulement s'il existe une base de F₁ et une base de F₂ qui, mises bout à bout, forment une famille libre.

Cas de la dimension finie : lorsque F₁ et F₂ sont de dimensions finies, la somme F₁ + F₂ est directe si et seulement si .

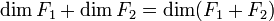
Sous-espaces supplémentaires : deux sous-espaces F₁ et F₂ de E sont dits supplémentaires lorsque . Cela signifie que pour tout élément u de E, il existe un unique couple de tel que .

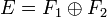
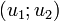
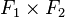
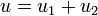
Somme directe de plusieurs sous-espaces vectoriels

On peut généraliser la notion de somme directe à une famille finie de sous-espaces vectoriels de E.

On dit qu'une famille de sous-espaces vectoriels de E est en somme directe si et seulement si, pour tout élément u de la somme , il existe un k-uplet unique de tel que .

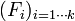
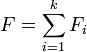
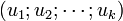
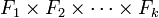
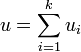
On dit aussi dans ce cas que la somme F des sous-espaces est directe.

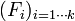
En d'autres termes, la somme est directe si la décomposition de tout élément de en somme d'éléments des est unique.

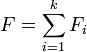
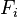
Pour désigner une somme directe, on se sert des notations ou .

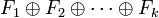
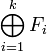
Comme dans le cas de 2 sous-espaces vectoriels, on peut caractériser les sommes directes par l'unicité de la décomposition du vecteur nul :

La somme est directe si et seulement si :

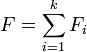
l'unique k-uplet de tel que est celui dont tous les éléments sont nuls.

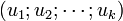
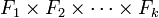
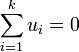
Remarque : dès que la famille comprend au moins 3 sous-espaces, il ne suffit pas pour que la somme soit directe que leurs intersections deux à deux soient réduites à , c'est-à-dire que :

pour tout i et pour tout j, i différent de j.

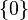
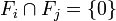
On s’en convaincra en regardant dans les sous-espaces vectoriels :

.

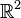
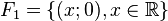
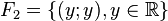
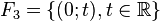
Leurs intersections deux à deux sont réduites à {(0 ; 0)}, mais leur somme (égale à ) n'est pas directe.

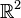
En effet, les 3 vecteurs appartiennent respectivement à  ; ils sont non nuls, et tels que : la décomposition du vecteur nul n'est pas unique.

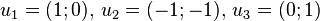
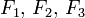
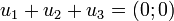
En revanche, on montre que les sous-espaces de la famille des sont en somme directe dans si et seulement si :

• 
• 

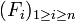
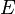
Lorsque les sous-espaces vectoriels sont de dimensions finies, on a encore l'équivalence des assertions suivantes :

1. Les sont en somme directe.
2. .
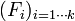
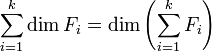
3. En concaténant une base de , ... , une base de , on constitue une base de la somme.

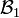
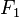
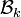
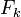
Exemple : soient E un espace vectoriel sur K de dimension finie, et f un endomorphisme de E ayant exactement p valeurs propres (distinctes) appelées . On désigne par l'endomorphisme identique de E.

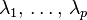
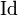
Pour tout entier i tel que 1 ≤ i ≤ p, est le sous-espace propre de f associé à la valeur propre .
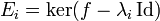
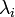
Les deux propriétés suivantes sont classiques :

• La somme est directe.
• si et seulement si f est diagonalisable.

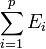
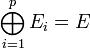
Lorsque c'est le cas, on constitue une base de E diagonalisant f en concaténant une base de , ... , une base de .

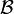
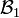
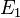
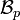
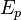
Somme directe orthogonale

On désigne ici par E un espace préhilbertien réel ou complexe (espace vectoriel réel ou complexe muni d'un produit scalaire). Soit une famille de sous-espaces vectoriels de E. S'ils sont deux à deux orthogonaux, leur somme est directe. Elle est alors appelée somme directe orthogonale.

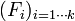
Un exemple très simple est l'espace constitué des vecteurs orthogonaux à tous les vecteurs d'un sous-espace vectoriel F : il est en somme directe avec F. L'égalité n'est pas toujours vérifiée lorsque la dimension est infinie. Par contre, elle l'est dès que E est de dimension finie.

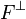
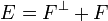
Deux espaces qui sont à la fois supplémentaires et orthogonaux sont dits supplémentaires orthogonaux. Un sous-espace vectoriel F de E, même s'il a des supplémentaires, n'en a pas nécessairement un qui lui soit orthogonal. Une condition suffisante est que l'espace F soit complet (ce qui est réalisé en particulier s'il est de dimension finie). Cette question est liée à la possibilité d'effectuer une projection orthogonale.

Lorsque les sous-espaces vectoriels sont de dimensions finies, on a l'équivalence des assertions suivantes :

1. Les sont en somme directe orthogonale.
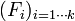
2. En concaténant une base orthogonale de , ... , une base orthogonale de , on constitue une base orthogonale de la somme.