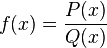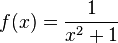Fonction rationnelle - Définition

En mathématiques, une fonction rationnelle est un rapport de fonctions polynômes à valeurs dans un corps K. En pratique, ce corps est généralement (corps des réels) ou (corps des complexes). Si P et Q sont deux fonctions polynômes et si Q n'est pas une fonction nulle, la fonction est définie pour tout x tel que par

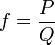
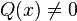
Domaine de définition

Toute fonction polynôme non-nulle Q est acceptable mais la possibilité que pour un a donné, Q(a) = 0 implique que contrairement aux fonctions polynomiales, les fonctions rationnelles n'ont pas un domaine de définition toujours égal à K.

Les racines du polynôme Q sont appelées pôles de la fonction rationnelle.

Exemple : soit

cette fonction est définie pour tout nombre réel x mais elle ne l'est pas pour tous les nombres complexes. Le dénominateur est 0 quand x = i et quand x = − i, où i est l'unité imaginaire.

Utilisations

Les fonctions rationnelles sont utilisées en analyse numérique pour faire l'interpolation et le lissage de fonctions. L'approximation est bien adaptée aux logiciels d'algèbre symbolique et de calculs numériques car tout comme les polynômes, elle peuvent être évaluées efficacement tout en étant plus expressives que ceux-ci.

Décomposition en éléments simples

Toute fonction rationnelle se décompose sous la forme de la somme d'un polynome et de fractions dont les dénominateurs sont des polynomes premiers et dont le degré du numérateur est inférieur à celui du dénominateur.

En pratique, dans , toute fonction rationnelle se décompose sous la forme de la somme d'une fonction polynôme et de fonction de type . Dans , toute fonction rationnelle se décompose sous la forme de la somme d'une fonction polynôme et de fonctions de types ou

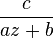
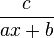
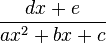
La décomposition en éléments simples permet de faciliter le calcul d'intégrales.

Fonction rationnelle et fraction rationnelle

Du point de vue mathématique, il faut distinguer le polynôme qui est d'abord une expression formelle et la fonction polynôme sur un domaine donné. Ceci est également vrai pour les quotients de polynômes. En algèbre générale, on appelle fraction rationnelle un élément du corps des fractions d'un anneau de polynômes. Pour poser cette définition, on doit partir d'un domaine d'intégrité (anneau commutatif unitaire intègre) R puis construire

,

l'anneau des polynômes en X, Y,..., T. Cet anneau sera aussi un domaine d'intégrité. Il est alors possible de construire le corps des fractions de cet ensemble appelé ensemble des fractions rationnelles à coefficients dans R et d'indéterminées X, Y ,... T