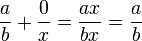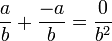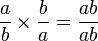Corps des fractions - Définition

Introduction

En théorie des anneaux, le corps des fractions d'un anneau A commutatif, intègre et non nul, est le plus petit corps (à isomorphisme près) contenant A.

Sa construction est une généralisation à un anneau de la construction du corps des rationnels à partir de l'anneau des entiers relatifs. Appliqué à un anneau de polynômes, il permet la construction de son corps des fractions rationnelles.

Cette construction se généralise encore avec le procédé de localisation.

Construction

On définit sur E = A × A\{0} deux lois internes et une relation d'équivalence compatible avec ces deux lois :

• une pseudo-addition : pour tout (a , b) et (c , d) de E , (a , b) + (c , d) = (ad + cb , bd)
• une pseudo-multiplication : pour tout (a , b) et (c , d) de E, (a , b) . (c , d) = (ac , bd)
• une relation : pour tout (a , b) et (c , d) de E, (a , b) ~ (c , d) si ad = bc.

L'existence des deux lois est fortement subordonnée au fait que l'anneau soit intègre car il faut que le produit bd soit non nul. Dans ce cas, les deux lois de composition interne sont bien définies, commutatives (d'après la commutativité du produit sur A) et associatives. Elles ne possèdent un neutre que si l'anneau est unitaire (il s'agit dans ce cas de (0, 1) pour la première et (1, 1) pour la seconde) et même dans ce cas, si l'anneau n'est pas déjà un corps, il existe des éléments sans inverse pour aucune des deux lois construites sur E. Enfin, il n'y a pas de distributivité de la seconde loi sur la première.

La relation ~ définie par (a , b) ~ (c , d) si ad = bc est bien symétrique, réflexive et transitive par hypothèse d'intégrité. Elle est de plus compatible avec les deux lois, c'est-à-dire que la classe du résultat de la pseudo-multiplication (ou de la pseudo-addition) ne dépend que des classes des opérandes. Autrement dit, les lois de composition peuvent être appliquées aux classes d'équivalence sans tenir compte du choix du représentant.

La classe d'un couple (a , b) se note usuellement et est appelée fraction.

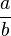
L'ensemble quotient, noté K(A) est muni des lois de composition induites (addition et multiplication).

Exemple

La construction des nombres rationnels consiste à définir le corps Q des nombres rationnels comme le corps des fractions de l'anneau Z des entiers relatifs.

Propriétés

Corps

K(A) est alors un corps commutatif, c'est-à-dire qu'il possède les propriétés suivantes (on fixe un élément non nul quelconque x de A) :

• simplification de fraction : pour tout c non nul,  ;
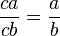
• commutativité et associativité des lois induites ;
• existence d'un neutre pour la première loi

• existence d'une unité neutre pour la seconde ;

• existence d'un opposé pour tout élément  ;

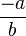
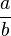
• existence d'un inverse pour tout élément non nul  ;

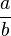
• distributivité de la multiplication sur l'addition :

Plongement

Si l'anneau A est unitaire, l'application i de A dans K(A) qui, à l'élément a, associe est un morphisme injectif qui plonge l'anneau A dans son corps de fractions.

Si l'anneau A n'est pas unitaire, on choisit un élément e non nul de A. L'application i de A dans K(A) qui, à l'élément a associe est un morphisme injectif qui plonge l'anneau A dans son corps de fractions. Cette application ne dépend pas de l'élément e non nul choisi.

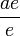
Propriété universelle

Pour tout corps L et tout morphisme injectif d'anneaux de A dans L, il existe un unique morphisme de corps de K(A) dans L tel que

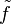
La seule façon de créer est de définir par , où e est un élément non nul fixé de A. Il suffit ensuite de prouver que cette construction est indépendante du représentant choisi et que est bien un morphisme injectif.

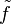
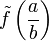
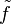
Unicité

D'après la propriété universelle, K(A) est le plus petit corps contenant A. En effet, si L est un autre corps contenant A, il existe un morphisme injectif de A dans L donc un morphisme injectif de K(A) dans L.