Décodage par syndrome - Définition

Capacité de correction

Distance de Hamming

La distance de Hamming est l'outil de base de la correction des erreurs. Elle s'exprime comme une distance issue d'une pseudo-norme. Le poids de Hamming, qui à un code associe le nombre de coordonnées non nulles, joue ici le rôle de pseudo-norme.

• Si ω désigne le poids de Hamming pour un code linéaire C, alors la distance de Hamming d est définie par la formule suivante:

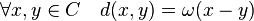
La linéarité de la structure sous-jacente introduit une propriété directe:

• La distance minimale δ entre deux points du code est égale au minimum du poids des mots du code non nuls.

Pour s'en convaincre, il suffit de remarquer que si x et y sont deux mots du code, alors leur différence est aussi un mot du code.

Ainsi, si un message reçu x n'est pas un mot de code, alors des altérations se sont produites durant la transmission. L'objectif est de trouver l'élément e de F de plus petit poids de Hamming, tel que x - e est un mot du code. Si la probabilité de recevoir p erreurs lors d'une transmission est une fonction décroissante de p, alors la correction est la plus probable.

Code parfait

Le nombre maximum d'erreurs assurément corrigibles t découle directement de la distance minimale δ. En effet, t est le plus grand entier strictement inférieur à δ/2. La situation idéale est celle où les boules fermées de centre les mots du code et de rayon t forment une partition de F. On parle alors de parfait.

Si le message reçu contient plus de t erreurs, une alternative se présente :

• Dans la mesure du possible, par exemple pour la téléphonie mobile une demande de retransmission est faite en temps masqué.
• Sinon, par exemple dans le cas du disque compact, un mot du code proche et aléatoirement choisi est sélectionné.

Limite de l'approche

L'approche du décodage par syndrome est adapté aux petits codes, c’est-à-dire ceux où le nombre t d'erreurs assurément corrigibles n'est pas trop important. On peut citer par exemple certains protocoles utilisés par internet comme le TCP ou encore le minitel qui utilise un code parfait de dimension 127 distance minimale égale à 7.

En revanche, un code possédant une redondance forte, et capable de résister à des effacements importants, ne peut utiliser cette technique de décodage. La norme utilisée par la société Philips pour le code des disques compacts est à même de restituer 4096 bits manquants. La capacité de stockage d'un lecteur est largement trop faible pour stocker les syndromes. D'autres techniques, essentiellement fondées sur l'étude des polynômes formels à coefficients dans un corps fini représentent les approches les plus utilisées par l'industrie.