Décodage par syndrome - Définition

Introduction

Le décodage par syndrome est une méthode de décodage destinée aux codes linéaires. Il utilise une table, appelée tableau standard, pour effectuer le décodage. Il est utilisable lorsque la redondance du code n'est pas trop grande : la taille de la table est exponentielle en la redondance.

Le principe est le suivant : à la réception d'un mot x, la matrice de contrôle permet de déterminer si une altération a été commise. Si tel est le cas, la matrice de contrôle fournit une quantité appelée syndrome ; le tableau standard offre une correspondance entre ce syndrome et la correction e à apporter. Le message corrigé est alors égal à x - e.

Contexte

Code correcteur

Un code correcteur possède pour objectif la détection ou la correction d'erreurs après la transmission d'un message. Cette correction est permise grâce à l'ajout d'informations redondantes. Le message est plongé dans un ensemble plus grand, la différence de taille contient la redondance, l'image du message par le plongement est transmis. En cas d'altération du message, la redondance est conçue pour détecter ou corriger les erreurs. Un exemple simple est celui du code de répétition, le message est, par exemple, envoyé trois fois, le décodage se fait par vote. Ici, l'ensemble plus grand est de dimension triple à celle du message initial.

Code linéaire

Rappelons les éléments de base de la formalisation. Il existe un espace vectoriel E constitué de suites à valeurs dans un corps fini F_d et de longueur k, c’est-à-dire qu'à partir du rang k, toutes les valeurs de la suite sont nulles. Ces éléments sont l'espace des messages que l'on souhaite communiquer. Pour munir le message de la redondance souhaitée, il existe une application linéaire φ injective de E à valeurs dans F, l'espace des suites de longueur n à valeurs dans F_d. La fonction φ est appelée encodage, φ(E) aussi noté C est appelé le code, un élément de φ(E) mot du code, k la longueur du code et n la dimension du code. Ces notations sont utilisées dans tout l'article.

Fonctionnement détaillé

Décodage et linéarité

La linéarité simplifie grandement le décodage. Pour s'en rendre compte, le plus simple est d'étudier un exemple. Considérons un code utilisé par le minitel, binaire de dimension 127 de longueur 120 et de distance minimale 3 et parfait. Si un message m est codé puis envoyé au récepteur, un élément x de F est reçu, susceptible d'erreur.

Le nombre t d'erreurs maximales assurément corrigibles est le plus grand entier strictement inférieur à 3/2 c’est-à-dire t = 1. Comme le code est parfait, les boules fermées de centre les mots du code et de rayon un forment une partition de F. En conséquence, x s'écrit de manière unique sous la forme c + e où c est un mot du code et e un élément de F de poids inférieur ou égal à un. Si la probabilité d'obtenir p erreurs durant la transmission est une fonction décroissante de p, c est probablement égal φ(m).

L'ensemble des valeurs possibles de e est relativement faible, ici comme le code est binaire, soit e est le vecteur nul, et aucune correction n'est à apporter, soit e est de poids un, c’est-à-dire que e est le message ne contenant que des zéros sauf sur une des 127 coordonnées qui vaut un. Il n'existe finalement que 128 cas d'erreurs dans un espace contenant 2¹²⁷ éléments.

La linéarité permet de se limiter à la connaissance de l'unique boule fermée de centre zéro et de rayon t, soit dans l'exemple à une boule de 128 points. Dans le cas général, une boule fermée de rayon t à pour cardinal V_t (cf borne de Hamming):

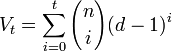
Implémentation

La théorie des codes correcteurs affirme l'existence d'une application linéaire surjective de F dans un espace de dimension n - k dont la matrice H est appelée matrice de contrôle et dont le noyau est le code. En conséquence, on dispose des égalités suivantes :

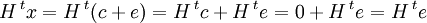
Dans le cas d'un code parfait, la restriction de H à la boule fermée de centre le vecteur nul et de rayon t est une bijection. Ici, la matrice H est identifiée à son application linéaire. Dans le cas du minitel, la boule unité contient 128 points, l'ensemble d'arrivée de H est un espace de dimension 7 et donc aussi de cardinal 128.

• L'élément H.^tx est appelé syndrome du point x de F.

La donnée d'une table, dite tableau standard associant à chaque syndrome son unique antécédent par H dans la boule de centre le vecteur nul et de rayon t, permet le décodage. La correction d'erreurs consiste à soustraire l'antécédent e à l'élément de F reçu. Le mot du code recherché est c = x - e. L'implémentation informatique de cette méthode utilise une table de hachage et constitue une méthode rapide de décodage.

Dans le cas général, en plus de la valeur t du nombre maximal d'erreur assurément corrigibles, il est nécessaire de considérer la plus petite valeur s tel que les boules fermées de centre les points du code et de rayon s forment un recouvrement de F. Un code est parfait si et seulement si s est égal à t. H possède alors les propriétés suivantes :

• La restriction de H à la boule de centre le vecteur nul et de rayon t est injective, la restriction de H à la boule de centre le vecteur nul et de rayon t est surjective.

Il existe alors deux méthodes de décodages si H.^tx n'admet pas d'antécédent dans la boule fermée de rayon t, soit une nouvelle demande de transmission est réalisée, soit un antécédent est choisi aléatoirement dans la boule fermée de rayon s, et la méthode reste la même. Dans tous les cas, le tableau standard contient d^n-k entrées où d est le cardinal du corps fini.